
4.数据2,-1,0,-3,-2,3,1的样本标准差为_____________.
[提示]这组数据的方差怎么求?它的标准差与方差有什么关系?
[答案]2.
[点评]本题考查方差、标准差的求法,由
s2=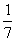 [22+(-1)2+02+(-3)2+(-2)2+32+12-7×0]=4,
[22+(-1)2+02+(-3)2+(-2)2+32+12-7×0]=4,
故 s=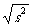 =2.
=2.
或由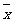 =0知,
=0知,
s 2=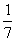 [22+(-1)2+02+(-3)2+(-2)2+32+12]=4,
[22+(-1)2+02+(-3)2+(-2)2+32+12]=4,
故 s=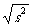 =2.
=2.
3.在数据-1,0,4,5,8中插入一个数x,使这组数据的中位数为3,则x=_______.
[提示]插入一个数据后共有几个数据?此时中位数应如何求得?
[答案]2.
[点评]本题考查中位数意义的灵活运用.因为加一个数据后有六个数,故中位数应为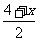 ,即
,即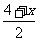 =3,所以x=2.
=3,所以x=2.
2.n个数据的和为56,平均数为8,则n=__________.
[提示]平均数=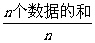 .
.
[答案]7.
[点评]本题考查平均数的意义.
1.某班的5位同学在向“救助贫困学生”捐款活动中,捐款数如下(单位:元):8,3,8,2,4,那么这组数据的众数是_______,中位数是_________,平均数是_______.
[答案]8,4,5.
[点评]本题考查众数、中位数、平均数的求法,因8出现两次,故众数为8;把数据按2,3,4,8,8排列,中位数即第三个数4;平均数为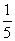 (8+3+8+2+4)=
(8+3+8+2+4)=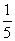 ×25=5.
×25=5.
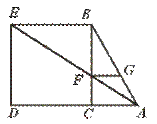
30.已知:如图,在△ABC中,∠C=90°,以BC为边向外作正方形BEDC,连结AE交BC于F,作FG∥BE交AB于G.
求证:FG=FC.
[提示]证明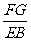 =
= .
.
[答案]∵ FG∥BE,∴ 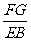 =
=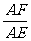 .∵ FC∥ED,∴
.∵ FC∥ED,∴  =
=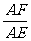 .
.
∴ 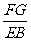 =
= .又 EB=ED,∴ FG=FC.
.又 EB=ED,∴ FG=FC.
29.如图,BD、CE为△ABC的高,求证∠AED=∠ACB.
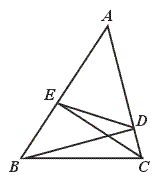
[提示]先证△ABD∽△ACE,再证△ADE∽△ABC.
[答案]∵ ∠ADB=∠AEC=90°,∠A=∠A,
∴ △ABD∽△ACE.∴ 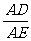 =
=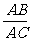 .
.
又 ∠A=∠A,∴ △ADE∽△ABC.∴ ∠AED=∠ACB.
[点评]本题要求运用相似三角形的判定与性质.
28.已知:如图,△ABC中,AB=AC,AD是中线,P是AD上一点,过C作CF∥AB,延长BP交AC于E,交CF于F.求证:BP2=PE·PF.
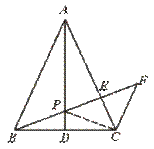
[提示]先证PB=PC,再证△EPC∽△CPF.
[答案]连结PC.
∵ AB=AC,AD是中线,∴ AD是△ABC的对称轴.
∴ PC=PB,∠PCE=∠ABP.∵ CF∥AB,
∴ ∠PFC=∠ABP.∴ ∠PCE=∠PFC.
又 ∠CPE=∠EPC,∴ △EPG∽△CPF.
∴ 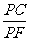 =
=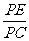 .即 PC2=PE·PF.∴ BP2=PE·PF.
.即 PC2=PE·PF.∴ BP2=PE·PF.
[点评]本题要求运用等腰三角形的性质以及相似三角形的判定与性质.
27.已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.求证:△ADQ∽△QCP.
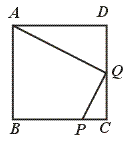
[提示]先证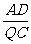 =
=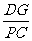 .
.
[答案]在正方形ABCD中,
∵ Q是CD的中点,∴ 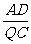 =2.
=2.
∵ 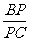 =3,∴
=3,∴ 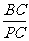 =4.
=4.
又 BC=2DQ,∴ 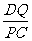 =2.
=2.
在△ADQ和△QCP中,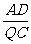 =
=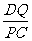 ,∠C=∠D=90°,
,∠C=∠D=90°,
∴ △ADQ∽△QCP.
[点评]本题要求运用相似三角形的判定定理.
26.如图,矩形PQMN内接于△ABC,矩形周长为24,AD⊥BC交PN于E,且BC=10,AE=16,求△ABC的面积.
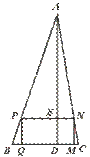
[提示]利用相似三角形的性质,列出关于ED的方程,求ED的长,即可求出S△ABC.
[答案]∵ 矩形PQMN,
∴ PN∥QM,PN=QM.∵ AD⊥BC,
∴ AE⊥PN.∵ △APN∽△ABC,
∴  =
=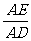 .
.
设ED=x,又 矩形周长为24,则
PN=12-x,AD=16+x.
∴ 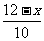 =
=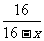 .即 x2+4x-32=0.解得 x=4.
.即 x2+4x-32=0.解得 x=4.
∴ AD=AE+ED=20.∴ S△ABC=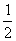 BC·AD=100.
BC·AD=100.
[点评]本题要求运用相似三角形对应高线的比等于相似比.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com