二

已知一个二次函数的图象经过A(-2,)、B(0,)和C(1,-2)三点。

(1)求出这个二次函数的解析式； (2)通过配方，求函数的顶点P的坐标；　

(3)作出函数的图象；　　　　　 　(4)若函数的图象与x轴相交于点E、F，(E在F的左边)求四边形EBPF的面积及cosF的值

函数及其图象测试答案

4．在生产中，为了节约原材料，加工某些零件时常利用一些边角废料，如图所示，△ABC为锐角三角形废料板，其中BC＝12㎝，BC边上的高AD＝8㎝。在△ABC上截取矩形PQMN,使QM边与BC边重合，PN交AD于F，设PQ长为x(㎝), 矩　　 形PQMN的面积为y(㎝²)　　

　 (1)用含x的代数式表示AF：AD的值和PN的长，　　 4分

　 (2)求y与x的函数关系式；　　　　　　 2分

(3)当x为多少时y取最大值？求出它的最大值，求出此时矩形的长和宽，并判断此时P落在AB边上的位置。　　　 4分

　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　 A

　　　　　　　　　 　　　　　　　　　　　　　　　　　P　　 F　　　 N

B　　　 Q　　 D　　 M　 C　

3．一次函数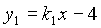与正比例函数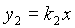的图象都经过点(2，1)

(1)分别求出这两个函数的解析式。　　 　　　　　　　3分

(2)作出两个函数的图象　　　　　　　　　　　　 3分

(3)求这两个函数图象与Y轴围成的三角形面积。　　 4分

2．已知直线L与直线y=2x+1的交点的横坐标为2，与直线y=-x+2的交点的纵坐标为1，求直线L的解析式。

1．已知直线和两坐标轴相交所围成的三角形面积为24，

求k值。

14． 已知二次函数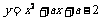．证明：不论a取何值，抛物线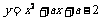的顶点Q总在x轴的下方；

13、 已知反比例函数(k≠0，k为常数)和正比例函数y=ax(a≠0，a为常数)。

(1)　　　 求反比例函数的图象和正比例函数的图象的交点坐标；

(2)　　　 顺次连结上述所得到点的多边形是什么多边形？并证明你的结论；

(3)　　　 上述多边形能否为正方形？若能请你找出条件；若不能请说明理由。

11、解方程：　　　　　　　　　 12、用换元法解方程：

10．已知二次函数与一次函数的图象相交于点(如图所示)，则能使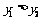成立的x的取值范围是________________．