例 5　 已知二次函y=ax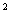+bx+c为x=2时有最大值2，其图象在X轴上截得的线段长为2，求这个二次函数的解析式。

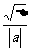
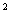分析　 弦长型的问题有两种思路，一是利用对称性求出交点坐标，二是用弦比公式d=就本题而言，可由对称性求得两交点坐标为A(1，0)，B(3，0)。再应用交点式或顶点式求得解析式为y=-2x+8x-6.

　　　 例 4　 二次函数y=x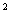+bx+c的图象向左平移两个单位，再向上平移3个单位得二次函数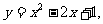则b与c分别等于

(A)2,-2;(B)-6,6;(c)-8,14;(D)-8,18.

分析　 逆用平移分式，将函数y=x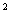-2x+1的顶点(1，0)先向下平移3个单位，再向右平移两个单位得原函数的图象的顶点为(3，-3)。

∴y=x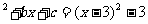

=x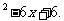

∴b=-6,c=6.

因此选(B)

　　　　 例 3　 已知抛物线y=ax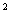+bx+c的顶点是A(-1,4)且经过点(1,2)求其解析式。

分析　 此类题型可设顶点坐标为(m,k)，故解析式为y=a(x-m)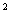+k.在本题中可设y=a(x+1)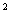+4.再将点(1,2)代入求得a=-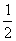

∴y=-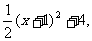

即y=-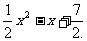

由于题中只有一个待定的系数a，将已知点代入即可求出，进而得到要求的解析式。

　　　 例2 已知抛物线y=-2x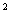+8x-9的顶点为A，若二次函数y=ax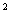+bx+c的图像经过A点，且与x轴交于B(0，0)、C(3，0)两点，试求这个二次函数的解析式。

分析　 要求的二次函数的图象与x轴的两个交点坐标，可设y=ax(x-3),再求也y=-2x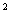+8x-9的顶点A(2，-1)。将A点的坐标代入y=ax(x-3),得到a=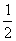

∴y=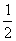x(x-3),即　 y=.

例1　　　　 已知一个二次函数图象经过(-1，10)、(2，7)和(1，4)三点，那么这个函数的解析式是_______。

　　 分析　 已知二次函数图象上的三个点，可设其解析式为y=ax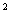+bx+c,将三个点的坐标代入，易得a=2,b=-3,c=5 。故所求函数解析式为y=2x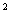-3x+5.

这种方法是将坐标代入y=ax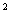+bx+c 后，把问题归结为解一个三元一次方程组，求出待定系数 a, b , c,　 进而获得解析式y=ax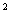+bx+c.

　　 ③　 略　 ④　 4.5,　

4. ⑴AF:AD=(8-X)/8 　　PN=3(8-X)/2　　 　⑵ y=-1.5x² +12x

　 ⑶　 y最大值为24,此时长为6,宽为4,p为AB的中点

3．① y=2.5x-4,　 y=0.5x　 ②略　 ③4/5

2．y=4x-3

1.y=3x+12,或y=-3x+12=