函数及其图象
例1.二次函数性质的应用
例2.利用二次函数性质求点的坐标
例3.求二次函数解析式
例4.求二次函数解析式
二、同步测试
三、提示与答案
--------------------------------------------------------------------------------
例6.已知抛物线y=ax2+bx+c如图所示,对称轴是直线x=-1
(1)确定a.b.c.b2-4ac的符号,
(2)求证a-b+c<o ;
(3)当x取何值时,y随x值的增大而减小。
解:(1)由抛物线开口向上,得出a>0,由抛物线与y轴交点坐标为(O,C),而此点在x轴下方,得出c<0,又由抛物线的对称轴是x=-1,在y轴左侧,得出b与a同号∴b>0。
抛物线与x轴有两个交点,即ax2+bc+c=0有两个不等的实根,∴b2-4ac>0
(2)当x=-1时,y=a-b+c<0
(3)当x<-1时,y随x值的增大而减小。
例7.已知y是x的二次函数,且其图象在x轴上截得的线段AB长4个单位,当x=3时,y取得最小值-2。(1)求这个二次函数的解析式 (2)若此函数图象上有一点P,使ΔPAB的面积等于12个平方单位,求P点坐标。
分析:由已知可得抛物线的对称轴是直线x=3,根据抛物线的对称性,又由抛物线在x轴上截得线段AB的长是4,可知其与x轴交点为(1,0),(5,0)
解:(1)∵当x=3时 y取得最小值-2.即抛物线顶点为(3,-2).∴设二次函数解析式为
y=a(x-3)2-2
又∵图象在x轴上截得线段AB的长是4,∴图象与x轴交于(1,0)和(5,0)两点
∴a(1-3)2-2=0 ∴a=
∴所求二次函数解析式为y= x2-3x+ x2-3x+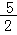
(2)∵ΔPAB的面积为12个平方单位,|AB|=4
∴ ×4×|Py|=12 ∴|Py|=6 ∴Pg=±6 ×4×|Py|=12 ∴|Py|=6 ∴Pg=±6
但抛物线开口向上,函数值最小为-2,∴Py=-6应舍去,∴Pg=6 又点P在抛物线上,
∴6= x2-3x+ x2-3x+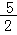
x1=-1,x2=7
即点P的坐标为(-1,6)或(7,6)
说明:此题如果设图象与x轴交点横坐标为x1,x2,运用公式|x1-x2|=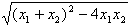 ,会使运算繁琐。这里利用抛物线的对称性将线段长的条件转化为点的坐标,比较简便。 ,会使运算繁琐。这里利用抛物线的对称性将线段长的条件转化为点的坐标,比较简便。
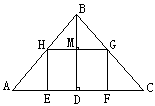
例8.如图,矩形EFGH内接于ΔABC。E、F在AC边上H、G分别在AB、BC边上,AC=8cm,高BD=6cm,设矩形的宽HE为x(cm)。试求出矩形EFGH的面积y(cm2)与矩形EFGH的宽x(cm)间的函数关系式,并回答当矩形的宽取多长时,它的面积最大,最大面积是多少?
解:∵四边形EFGH是矩形
∴HG∥AC
∴ΔABC∽ΔHBG
设BD交HG于M
则BD与BM分别是ΔABC和ΔHBG的高。
∴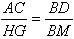
∵HG∥AC,
∴MD=HE=x,BM=6-x
∴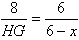 , ,
∴HG=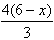
∵y=S矩形EFGH=HE*HG
∴y=x*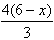
整理得y=-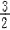 x2+8x x2+8x
∵BD=6
∴自变量x的取值范围是0<x<6
∵x2的系数为-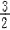 <0, <0,
∴y有最大值
当x=-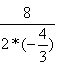 =3时, =3时,
y最大值=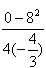 =12 =12
∴所求函数的解析式为y=-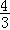 x2+8x(0<x<6),当它的宽为3cm时,矩形EFGH面积最大,最大面积为12cm2。 x2+8x(0<x<6),当它的宽为3cm时,矩形EFGH面积最大,最大面积为12cm2。
例9.二次函数y=ax2+bx-5的图象的对称轴为直线x=3,图象与y轴相交于点B,设x1,x2是方程ax2+bx-5=0的两个根,且x12+x22=26,又设二次函数图象顶点为A,
(1)求二次函数的解析式
(2)求原点O到直线AB的距离
解(1)如图 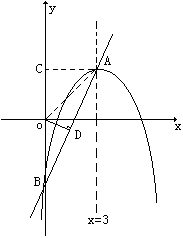
∵-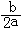 =3 ∴- =3 ∴-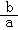 =6 =6
又x1+x2=-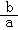 =6 =6
x1*x2=-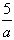
由已知,有x12+x22=26,
∴(x1+x2)2-2x1x2=26
即(-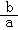 )2+ )2+ =26, =26, =26-36 =26-36
解得a=-1
∴解析式为y=-x2+6x-5=-(x-3)2+4
(2)∵OB=5,OC=4,AC=3
∴AB=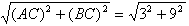 =3 =3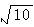
又OA=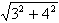 =5 =5
∴ΔAOB为等腰三角形,作OD⊥AB于D,
∴BD=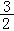 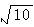
∴OD=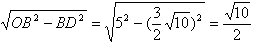 , ,
即原点O到直线AB的距离为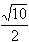
三、同步测试:
选择题:
1.如果点P(3m-p,1-m)是第三象限的整数点,那么P点坐标是( )
(A).(-2,-1) (B)(-3,-1)
(C)(-3,-2) (D)(-4,-2)
2.若点P(a,b)在第二、四象限两轴夹角平分线上,则a与b的关系是()
(A)a=b (B)a=-b (C)a=|b|
(D)|a|=b
3.点P(x,y)在第二象限,且|x|=2,|y|=3,则点P关于x轴对称点的坐标为( )
(A)(-2,3) (B)(2,-3)
(C)(-2,-3) (D)(2,3)
4.函数y= 中,自变量x的取值范围是( ) 中,自变量x的取值范围是( )
(A)x≤2 (B)x<2 (C)x≠2 (D)x>2
5.函数y=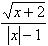 中,自变量x的取值范围是( ) 中,自变量x的取值范围是( )
(A)x>-2且x≠1 (B)x≥-2且x≠1
(C)x≥-2且x≠±1 (D)x≥-2或x≠±1
6.在下列函数中,成正比例函数关系的是( )
(A)圆的面积与它的周长
(B)矩形面积是定值,矩形的长与宽
(C)正方形面积与它的边长
(D)当底边一定时,三角形面积与底边上的高
7.函数y=k(x-1)与y=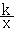 (k<o)在同一坐标系下的图象大致如图( ) (k<o)在同一坐标系下的图象大致如图( )
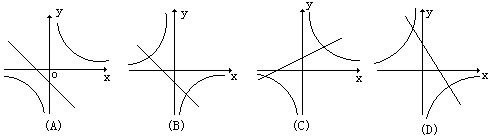 8.如果直线y=kx+b的图象过二、三、四象限,那么( )
8.如果直线y=kx+b的图象过二、三、四象限,那么( )
(A)k>0,b>0 (B) k>0,b<0
(C)k<0,b>0 (D)k<0,b<0
9.对于抛物线y=-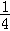 +x-x2,下列结论正确的是( ) +x-x2,下列结论正确的是( )
(A)开口向上,顶点坐标是( ,0) ,0)
(B)开口向下,顶点坐标是( ,0) ,0)
(C)开口向下,顶点坐标是(- , , ) )
(D)开口向上,顶点坐标是(-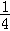 ,- ,- ) )
10.若a>0,b<0则函数y=ax2+bx的图象是下面图中的( )
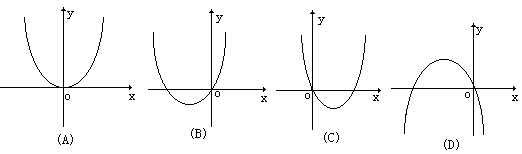 11.已知:二次函数y=ax2+bx+c的图象如图,则( )
11.已知:二次函数y=ax2+bx+c的图象如图,则( )
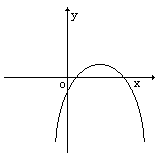
(A)a>0,b>0, c>0,Δ<0
(B)a<0,b>0, c<0,Δ>0
(C)a>0,b<0, c<0,Δ>0
(D)a<0,b<0, c>0,Δ<0
12.把函数y=2x2-4x-5的图象向左平移2个单位,再向下平移3个单位后,所得到的函数图象的解析式为( )
(A)y=2x2+4x-8 (B)y=2x2-8x+8
(C)y=2x2+4x-2 (D)y=2x2-8x-2
填空题
13.点A(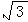 ,-5)到x轴的距离是____;到y轴的距离是____;到原点的距离是____. ,-5)到x轴的距离是____;到y轴的距离是____;到原点的距离是____.
14.直线y=kx+b与直线y=- x平行,且通过点(2,-3),则k=__,在y轴上的截距为___. x平行,且通过点(2,-3),则k=__,在y轴上的截距为___.
15.一次函数的图象经过(1,-5)点且与y轴交于(0,-1)点,则一次函数的解析式为____.
16.已知抛物线的顶点为M(4,8)且经过坐标原点,则抛物线所对应的二次函数的解析式为____.
解答题:
17.一次函y=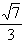 x+ x+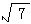 分别与x轴,y轴交于点A,B,点C(0,a)且a<0,若∠BAC为直角,求图象过点C与点A的一次函数解析式。 分别与x轴,y轴交于点A,B,点C(0,a)且a<0,若∠BAC为直角,求图象过点C与点A的一次函数解析式。
18.已知如图,在ΔABC中,AB=4,AC=6,D是AB边上一点,E是AC边上一点,∠ADE=∠C,设DB=x,AE=y。
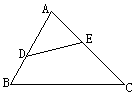
(1)求出y与x的函数关系式;
(2)画出这个函数图象。
19.在直角坐标系xoy中,直线l过点(4,0),且与x,y轴围成的直角三角形面积为8,一个二次函数图象过直线l与两坐标轴的交点,且以x=3为对称轴,开口向下。求二次函数的解析式及函数的最大值。
20.已知抛物线y=x2-mx+(2m+3)(m是不小于-2的整数)与x轴相交于A、B两点,且A、B两点间的距离恰是顶点到y轴距离的2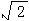 倍。 倍。
(1)求这条抛物线的函数解析式;
(2)如果D(t,2)是抛物线上一点且在第一象限,求D点坐标。
四.提示与答案
1.B 2.B 3.C 4.B 5.C 6.D 7.A 8.D
9.B 10.C 11.B 12.A 13.5,3,2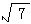
14.- ,-2 15.y=-4x-1 16.y=- ,-2 15.y=-4x-1 16.y=- x2+4x x2+4x
17.y=-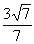 x- x-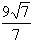
18.(1)y=- x+ x+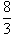 (0≤x<4);(2)图略 (0≤x<4);(2)图略
19.y=- x2+3x-4,最大值为 x2+3x-4,最大值为 . .
20.(1)y=x2+2x-1;(2)D(1,2)
|
|

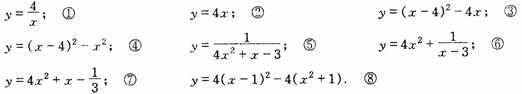
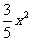 ;②
;②
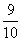 x2; ⑤ y=4x2.⑥
x2; ⑤ y=4x2.⑥
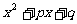 与x轴交于A、B两点,与y轴交于C点,
与x轴交于A、B两点,与y轴交于C点,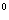 ,且tg∠CAO-tg∠CBO=2,求其解析式.
,且tg∠CAO-tg∠CBO=2,求其解析式.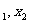 ,则q=(-x
,则q=(-x
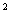 =OA·OB,
=OA·OB,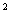 =q解得q
=q解得q =1,q
=1,q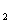 =0(舍去),
=0(舍去),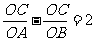
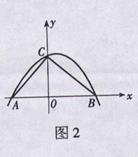

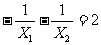
 +x
+x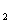 =-2x
=-2x x
x  即 p=2p=2
即 p=2p=2 +2x+1
+2x+1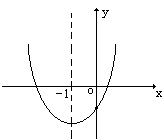
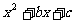 的图象经过三点(0,
的图象经过三点(0,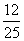 )、(sinA,0)、(sinB,0)且A、B为直角三角形的两个锐角,求其解析式。
)、(sinA,0)、(sinB,0)且A、B为直角三角形的两个锐角,求其解析式。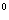 ,∴sinB=cosA.
,∴sinB=cosA.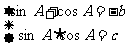
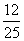 )代入解析式,得c=
)代入解析式,得c=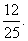
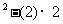 ,得
,得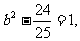 ∴
∴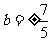
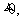 ∴b=-
∴b=-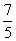
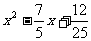
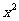 -mx+2m-4如果抛物线与x轴相交的两个交点以及抛物线的顶点组成一个等边三角形,求其解析式。
-mx+2m-4如果抛物线与x轴相交的两个交点以及抛物线的顶点组成一个等边三角形,求其解析式。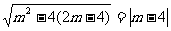
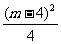
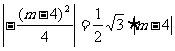
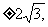 故所求解析式为
故所求解析式为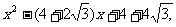

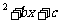 的对称轴在 y轴的右侧,且抛物线与 y轴交于Q(0,-3),与x轴的交点为A、B,顶点为P,ΔPAB的面积为8。求其解析式。
的对称轴在 y轴的右侧,且抛物线与 y轴交于Q(0,-3),与x轴的交点为A、B,顶点为P,ΔPAB的面积为8。求其解析式。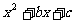 得 c=-3.
得 c=-3.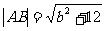
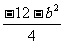

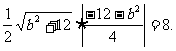
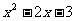
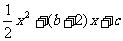 与y=
与y=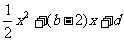 其中一条的顶点为P,另一条与X轴交于M、N两点。
其中一条的顶点为P,另一条与X轴交于M、N两点。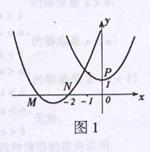
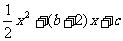 与x轴交于M,N两点(过程从略);
与x轴交于M,N两点(过程从略);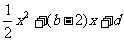 的顶点坐标为(0,1),
的顶点坐标为(0,1),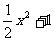 .
.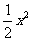 +(b+2)x+c得c=6.
+(b+2)x+c得c=6.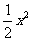 +4x+6
+4x+6