8.y=-5x²图象开口向下，有最大值.这个最大值是0.

　课堂教学设计说明

　这节课要使学生明了y=ax²，的图象是抛物线，这是研究一般二次函数图象的基础.能过列表及画图，要使学生理解y=ax²的性质.

　本节课在一开始，由三个实际问题引出三个不同形式的解析式y=6x²,y=-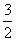x²+30x,y=200x²+400x+200.然后介绍二次函数一般式的定义.并设计了例1，让学生辨认哪个是二次函数.

　接着讲解y=x²的图象画法(这是画抛物线的基本步骤，务必掌握)，并总结出的性质.

　为了说明y=ax²中系数a对图形影响，设计了例2，并作出了规律性的结论，例2的相互制约的思想.还培养学生以运动的运动的观点来认识事物.

　例3的设计思想是求函数y=ax²的解析式，利用“点在图象上相当于上点的坐标适合函数式”这个数形结合的思想，各利用特定系数法求系数a.再利用上述数形结合思想，判断某点是否在图像上及已知点的纵坐标求横坐标.

　作业中补充的第1题，综合了二次函数与一次函数对图形的影响.补充的第3题仅加深了

二次函数概念，还训练学生审题的能力(应舍去m=4).

6.y=(3+x)²-3²=x²+6x.

　.

5.是正比例函数的有②，⑧，是一次函数的有②，④，⑧，是二次函数的有③，⑦.

4.(1)a=0且c=0且b≠0;　　 (2)a=0且b≠0;　 (3)a≠0.

3.令m²-5m+6=2,得m=1,m=4(舍去).m=1时，y=-3x².

2.(1)开口向上的有②，③，⑥；(2)开口向下且开口最大的是⑤；(3)①，④，⑤.

1.选(C).因为在(A)中，直线的a＞0而抛物线的a＜0，不能成立.在(B)，(D)中，直线的b＞0与已知予盾.

8.从图象上看，函数y=-5x²有最大值还是有最小值?如果有，是最大值还是最小值?这个

值是多少?

　作业的答案或提示

7.已知函数y=ax²的图象过点(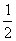,2).求此图象上纵坐标为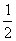时的点的坐标 .

6.正方形边长是3，若边长增加x，则面积增加y，求y与x之间的函数关系.