
3、 已知二次函数
已知二次函数 的图象过点A(
的图象过点A(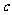 ,0),且关于直线
,0),且关于直线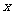 =2对称,则这个二次函数的解析式可能是
。(只要求写一个可能的解析式)
=2对称,则这个二次函数的解析式可能是
。(只要求写一个可能的解析式)
2、如果抛物线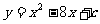 的顶点在
的顶点在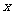 轴上,则
轴上,则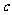 =
。
=
。
1、抛物线 的口向
,且有最 点。
的口向
,且有最 点。
例1.已知y=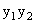 ,其中
,其中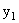 =
= (k≠0的常数),
(k≠0的常数),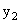 与
与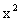 成正比例,求证y与x也成正比例。 证明:∵
成正比例,求证y与x也成正比例。 证明:∵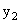 与
与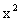 成正比例,
成正比例,
设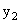 =a
=a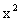 (a≠0的常数),
(a≠0的常数),
∵y=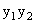 ,
, 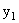 =
= (k≠0的常数),
(k≠0的常数),
∴y= ·a
·a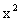 =akx,
=akx,
其中ak≠0的常数,
∴y与x也成正比例。
例2.已知一次函数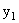 =(n-2)x+
=(n-2)x+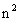 -n-3的图象与y轴交点的纵坐标为-1,判断
-n-3的图象与y轴交点的纵坐标为-1,判断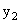 =(3-
=(3-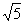 )
)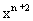 是什么函数,写出两个函数的解析式,并指出两个函数在直角坐标系中的位置及增减性。
是什么函数,写出两个函数的解析式,并指出两个函数在直角坐标系中的位置及增减性。
解:依题意,得 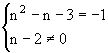
解得 n=-1,
∴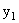 =-3x-1,
=-3x-1,
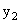 =(3-
=(3-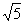 )x,
)x, 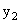 是正比例函数;
是正比例函数;
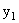 =-3x-1的图象经过第二、三、四象限,
=-3x-1的图象经过第二、三、四象限,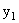 随x的增大而减小;
随x的增大而减小;
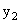 =(3-
=(3-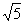 )x的图象经过第一、三象限,
)x的图象经过第一、三象限,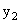 随x的增大而增大。
随x的增大而增大。
说明:由于一次函数的解析式含有待定系数n,故求解析式的关键是构造关于n的方程,此题利用“一次函数解析式的常数项就是图象与y轴交点纵坐标”来构造方程。
例3.直线y=kx+b与直线y=5-4x平行,且与直线y=-3(x-6)相交,交点在y轴上,求此直线解析式。
分析:直线y=kx+b的位置由系数k、b来决定:由k来定方向,由b来定与y轴的交点,若两直线平行,则解析式的一次项系数k相等。例 y=2x,y=2x+3的图象平行。
解:∵y=kx+b与y=5-4x平行,
∴k=-4,
∵y=kx+b与y=-3(x-6)=-3x+18相交于y轴,
∴b=18,
∴y=-4x+18。
说明:一次函数y=kx+b图象的位置由系数k、b来决定:由k来定方向,由b来定点,即函数图象平行于直线y=kx,经过(0, b)点,反之亦成立,即由函数图象方向定k,由与y轴交点定b。
例4.直线与x轴交于点A(-4,0),与y轴交于点B,若点B到x轴的距离为2,求直线的解析式。
解:∵点B到x轴的距离为2,
∴点B的坐标为(0,±2),
设直线的解析式为y=kx±2,
∵直线过点A(-4,0),
∴0=-4k±2,
解得:k=±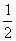 ,
,
∴直线AB的解析式为y=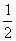 x+2或y=-
x+2或y=-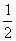 x-2.
x-2.
说明:此例看起来很简单,但实际上隐含了很多推理过程,而这些推理是求一次函数解析式必备的。
(1)图象是直线的函数是一次函数;
(2)直线与y轴交于B点,则点B(0,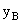 );
(3)点B到x轴距离为2,则|
);
(3)点B到x轴距离为2,则|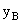 |=2;
(4)点B的纵坐标等于直线解析式的常数项,即b=
|=2;
(4)点B的纵坐标等于直线解析式的常数项,即b=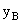 ;
(5)已知直线与y轴交点的纵坐标
;
(5)已知直线与y轴交点的纵坐标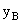 ,可设y=kx+
,可设y=kx+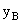 ,
下面只需待定k即可。
,
下面只需待定k即可。
例5.已知一次函数的图象,交x轴于A(-6,0),交正比例函数的图象于点B,且点B在第三象限,它的横坐标为-2,△AOB的面积为6平方单位,求正比例函数和一次函数的解析式。 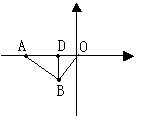
分析:自画草图如下:
解:设正比例函数y=kx,
一次函数y=ax+b,
∵点B在第三象限,横坐标为-2,
设B(-2,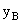 ),其中
),其中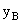 <0,
<0,
∵ =6,
=6,
∴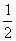 AO·|
AO·|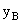 |=6,
|=6,
∴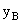 =-2,
=-2,
把点B(-2,-2)代入正比例函数y=kx,得k=1
把点A(-6,0)、B(-2,-2)代入y=ax+b,
得 
解得: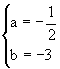
∴y=x, y=-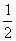 x-3即所求。
x-3即所求。
说明:(1)此例需要利用正比例函数、一次函数定义写出含待定系数的结构式,注意两个函数中的系数要用不同字母表示;
(2)此例需要把条件(面积)转化为点B的坐标。这个转化实质含有两步:一是利用面积公式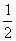 AO·BD=6(过点B作BD⊥AO于D)计算出线段长BD=2,再利用|
AO·BD=6(过点B作BD⊥AO于D)计算出线段长BD=2,再利用|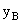 |=BD及点B在第三象限计算出
|=BD及点B在第三象限计算出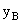 =-2。若去掉第三象限的条件,想一想点B的位置有几种可能,结果会有什么变化?(答:有两种可能,点B可能在第二象限(-2,2),结果增加一组y=-x, y=
=-2。若去掉第三象限的条件,想一想点B的位置有几种可能,结果会有什么变化?(答:有两种可能,点B可能在第二象限(-2,2),结果增加一组y=-x, y=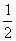 (x+3).
(x+3).
例6.已知正比例函数y=kx (k<0)图象上的一点与原点的距离等于13,过这点向x轴作垂线,这点到垂足间的线段和x轴及该图象围成的图形的面积等于30,求这个正比例函数的解析式。
分析:画草图如下:
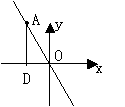 则OA=13,
则OA=13,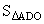 =30,
=30,
则列方程求出点A的坐标即可。
解法1:设图象上一点A(x, y)满足
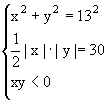
解得: ;
;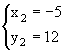 ;
;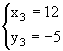 ;
;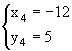
代入y=kx (k<0)得k=-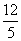 , k=-
, k=-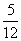 .
.
∴y=-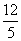 x或y=-
x或y=-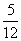 x。
x。
解法2:设图象上一点A(a, ka)满足
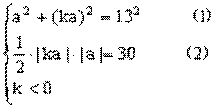
由(2)得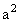 =-
=-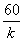 ,
,
代入(1),得(1+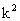 )·(-
)·(-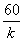 )=
)=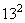 .
.
整理,得60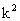 +169k+60=0.
+169k+60=0.
解得 k=-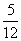 或k=-
或k=-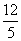 .
.
∴ y=-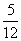 x或y=-
x或y=-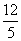 x.
x.
说明:由于题目已经给定含有待定系数的结构式y=kx,其中k为待定系数,故解此例的关键是构造关于k的方程。此例给出的两个解法代表两种不同的思路:解法1是把已知条件先转化为求函数图象上一点的坐标,构造方程解出,再求k;解法2是引进辅助未知数a,利用勾股定理、三角形面积公式直接构造关于a、k的方程组,解题时消去a,求出k值。
例7.在直角坐标系x0y中,一次函数y=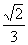 x+
x+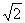 的图象与x轴,y轴,分别交于A、B两点,点C坐标为(1,0),点D在x轴上,且∠BCD=∠ABD,求图象经过B、D两点的一次函数的解析式。
的图象与x轴,y轴,分别交于A、B两点,点C坐标为(1,0),点D在x轴上,且∠BCD=∠ABD,求图象经过B、D两点的一次函数的解析式。
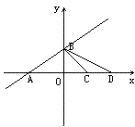
分析:由已知可得A点坐标(-3,0),B点坐标(0,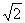 ),点C是确定的点(1,0),解题的关键是确定点D的坐标,由点D在x轴上,以∠BCD=∠ABD的条件,结合画草图可知∠BCD的边BC确定,顶点C确定,但边CD可以有两个方向,即点D可以在C点右侧,也可以在C点左侧,因此解此题要分类讨论。
),点C是确定的点(1,0),解题的关键是确定点D的坐标,由点D在x轴上,以∠BCD=∠ABD的条件,结合画草图可知∠BCD的边BC确定,顶点C确定,但边CD可以有两个方向,即点D可以在C点右侧,也可以在C点左侧,因此解此题要分类讨论。
解:∵点A、B分别是直线y=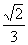 x+
x+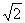 与x轴和y轴交点,
与x轴和y轴交点,
∴A(-3,0),B(0,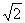 ),
),
∵点C坐标(1,0)由勾股定理得BC=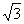 ,AB=
,AB=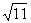 ,
,
设点D的坐标为(x, 0),
(1) 当点D在C点右侧,即x>1时,
当点D在C点右侧,即x>1时,
∵∠BCD=∠ABD,
∠BDC=∠ADB,
∴△BCD∽△ABD,
∴ =
=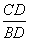
∴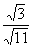 =
=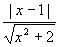 - - - - ①
- - - - ①
∴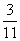 =
=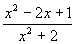
∴8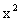 -22x+5=0
-22x+5=0
∴x1=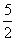 , x2=
, x2=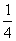 ,
,
经检验:x1=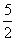 , x2=
, x2=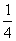 ,都是方程①的根。
,都是方程①的根。
∵x=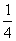 ,不合题意,∴舍去。∴x=
,不合题意,∴舍去。∴x=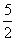 ,
,
∴D点坐标为(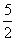 , 0)。
, 0)。
设图象过B、D两点的一次函数解析式为y=kx+b,
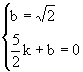 ∴
∴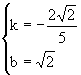
∴所求一次函数为y=-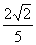 x+
x+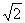 。
。
(2)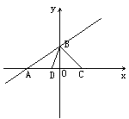 若点D在点C左侧则x<1,
若点D在点C左侧则x<1,
可证△ABC∽△ADB,
∴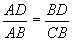
∴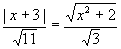 - - - - ②
- - - - ②
∴8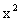 -18x-5=0
-18x-5=0
∴x1=-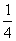 , x2=
, x2=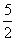 ,
,
经检验x1=-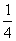 , x2=
, x2=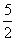 ,都是方程②的根。
,都是方程②的根。
∵x2=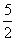 不合题意舍去,∴x1=-
不合题意舍去,∴x1=-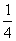 ,
,
∴D点坐标为(-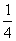 , 0),
, 0),
∴图象过B、D(-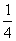 , 0)两点的一次函数解析式为y=4
, 0)两点的一次函数解析式为y=4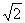 x+
x+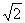 , s
, s
综上所述,满足题意的一次函数为y=-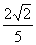 x+
x+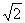 或y=4
或y=4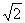 x+
x+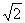 .
.
例8.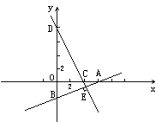 已知:如图一次函数y=
已知:如图一次函数y=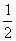 x-3的图象与x轴、y轴分别交于A、B两点,过点C(4,0)作AB的垂线交AB于点E,交y轴于点D,求点D、E的坐标。
x-3的图象与x轴、y轴分别交于A、B两点,过点C(4,0)作AB的垂线交AB于点E,交y轴于点D,求点D、E的坐标。
解:直线y=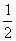 x-3与x轴交于点A(6,0),与y轴交于点B(0,-3),
x-3与x轴交于点A(6,0),与y轴交于点B(0,-3),
∴OA=6,OB=3,
∵OA⊥OB,CD⊥AB,
∴∠ODC=∠OAB,
∴cot∠ODC=cot∠OAB,即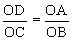
∴OD=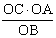 =
=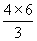 =8.
=8.
∴点D的坐标为(0,8),
设过CD的直线解析式为y=kx+8,将C( 4,0)代入
0=4k+8, 解得 k=-2
∴直线CD:y=-2x+8,
由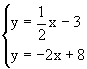 解得
解得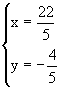
∴点E的坐标为(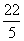 ,-
,-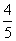 )
)
说明:由于点E既在直线AB上,又在直线CD上,所以可以把两直线的解析式联立,构成二元一次方程组,通过解方程组求得。
3.求一次函数解析式的方法
求函数解析式的方法主要有三种
一是由已知函数推导或推证
二是由实际问题列出二元方程,再转化为函数解析式,此类题一般在没有写出函数解析式前无法(或不易)判断两个变量之间具有什么样的函数关系。
三是用待定系数法求函数解析式。
“待定系数法”的基本思想就是方程思想,就是把具有某种确定形式的数学问题,通过引入一些待定的系数,转化为方程(组)来解决,题目的已知恒等式中含有几个等待确定的系数,一般就需列出几个含有待定系数的方程,本单元构造方程一般有下列几种情况:
(1)利用一次函数的定义
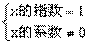
构造方程组。
(2)利用一次函数y=kx+b中常数项b恰为函数图象与y轴交点的纵坐标(如例6),即由b来定点;直线y=kx+b平行于y=kx,即由k来定方向(如例3)
(3)利用函数图象上的点的横、纵坐标满足此函数解析式构造方程(如例4、例5)。
(4)利用题目已知条件直接构造方程(如例6)
2.增减性
k>0时,y随x增大而增大
k<0时,y随x增大而减小
1.图象的位置:
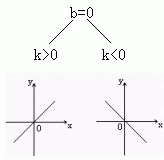
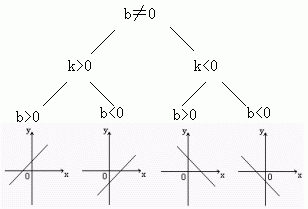
3、性质:
2、图象:一次函数的图象是一条直线,
(1)两个常有的特殊点:与y轴交于(0,b);与x轴交于(-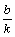 ,0)
,0)
(2)由图象可以知道,直线y=kx+b与直线y=kx平行,例如直线:y=2x+3与直线y=2x-5都与直线y=2x平行。
1、一次函数:形如y=kx+b (k≠0, k, b为常数)的函数。
注意:(1)k≠0,否则自变量x的最高次项的系数不为1;
(2)当b=0时,y=kx,y叫x的正比例函数。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com