
39.已知正比例函数y= (2 m –1 ) x的图象上的两点A(x1,y1), B (x2, y2),当x1< x时,有y1>y2那么m的取值范围是( )A m < 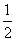 B m >
B m > 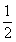 C m < 2 D m > 0
C m < 2 D m > 0
37.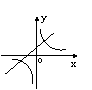
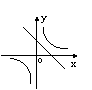
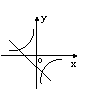
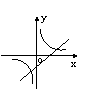 在同一直角坐标系中,函数y=
在同一直角坐标系中,函数y=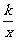 和y=kx+3 (k
和y=kx+3 (k 0)的图象大致是(
)
0)的图象大致是(
)
(A) (B) (C) (D)
38反比例函数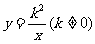 的图象的两个分支分别位于(
)
的图象的两个分支分别位于(
)
36.在直角坐标系xoy中,任意一点的横坐标与纵坐标互为倒数,则这点一定在( )
(A) 直线y = x上(B)直线y = - x 上
(B)
(C)双曲线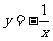 上(D)双曲线
上(D)双曲线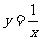 上
上
34.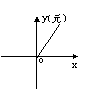

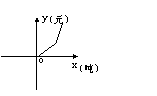
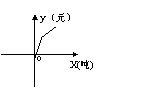 某城市为了节约用水,实行了价格调控,限定每户每月用水量不超过6(吨)时,每吨水价为2元;当用水量超过6吨时,超过的部分每吨的水价为3元。每户每月水费y(元)与用水量x(吨)的函数图象示意图是(
)
某城市为了节约用水,实行了价格调控,限定每户每月用水量不超过6(吨)时,每吨水价为2元;当用水量超过6吨时,超过的部分每吨的水价为3元。每户每月水费y(元)与用水量x(吨)的函数图象示意图是(
)
(A) (B) (C) (D)
|
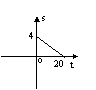
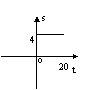
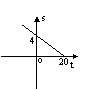 35. 土地沙漠是人类生存的大敌。某地现有绿地4万公顷,由于环保意识不强,植被遭到严重破坏,经观察土地沙化的速度为每年0.2万公顷,那么t年后,该地所剩绿地面积s(万公顷)与时间t(年)之间的函数关系用图象表示为( )
35. 土地沙漠是人类生存的大敌。某地现有绿地4万公顷,由于环保意识不强,植被遭到严重破坏,经观察土地沙化的速度为每年0.2万公顷,那么t年后,该地所剩绿地面积s(万公顷)与时间t(年)之间的函数关系用图象表示为( )
(A) (B) (C) (D)
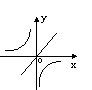
33.
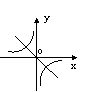
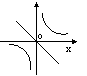
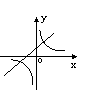 在同一直角坐标系中,函数y
= kx和
在同一直角坐标系中,函数y
= kx和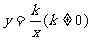 的图象只可能是(
)
的图象只可能是(
)
(A) (B) (C) (D)
32..若函数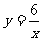 和
和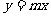 的图象都经过点(2,k ), 则这两个函数的图象还同时通过点(
)
的图象都经过点(2,k ), 则这两个函数的图象还同时通过点(
)
(A)(-2,-3) (B)(-3,-2) (C)(2,3) (D)(3 , 2)
30. 如果y与x2 成反比例,并且当x = 3 时,y = 4,那么当x = - 3 时,y的值为( )
(A)- 4
(B)4
(C) (D)
(D)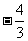
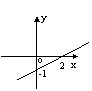 31 一次函数y= kx+b
的图象如图所示,则( )
31 一次函数y= kx+b
的图象如图所示,则( )
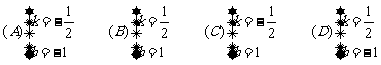
1 若P(4,2k-1)在第四象限内 ,则 k 的取值范围是( )
(A) k >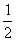 (B) k >-
(B) k >-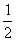 (C) k<
(C) k< 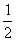 (D)
k < -
(D)
k < -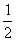
2点P(x,y)在第二象限,且│x│=2 ,│y│=3 ,则点P的坐标是( )
(A)(2 ,3) (B) (-2 ,3) ( C) (2 ,-3) ( D) (-2 ,-3)
3点P(-3,5)关于原点对称的点的坐标是( )
(A)(3,5) (B)(3,-5) (C)(-3,5) (D)(-3,-5)
4点(-3,1)关于x轴的对称点的坐标是( )
(A)(-3 ,-1) (B) (3 ,1) (C) (-3 ,-1) (D) (-3,1)
5 点A在X轴的负半轴上,它到原点的距离是5个单位长,则A点坐标是( )
(A)5 (B) -5 (C)(-5 ,0) (D) (0 ,- 5)
6 若点P(m ,n)是第一象限的点,则点(-m-1,n+2)在( )
(A)第一象限 (B)第二象限 (C)第三象限 (D)四象限
7 已知点A(a+2,4-b)、 B(2b+3,2a)是关于 x 轴的对称点,则a•b的值为( ) (A)-  (B)
(B)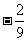 (C)6 (D)- 6
(C)6 (D)- 6
8 点P(m -2)与点Q(3,n)关于原点对称, 则m、n的值分别是( )
(A)-3,2 (B)3,-2 (C)-3,-2 (D) 3,2
9 函数y =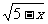 中,自变量 x 的取值范围是( )
中,自变量 x 的取值范围是( )
(A)x ≥0 (B)x≤-5 (C)x≥5 (D)x≤5
10 在函数y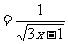 中, 自变量x 的取值范围是( )
中, 自变量x 的取值范围是( )
(A)x > 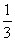 (B)x ≥
(B)x ≥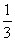 (C)x > 3 (D) x ≠
(C)x > 3 (D) x ≠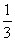
11 函数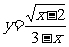 中, 自变量x 的取值范围是( )
中, 自变量x 的取值范围是( )
(A)x ≥2 (B)x≤2 (C)x≠3 (D)x ≥2且 x≠3
12 在函数
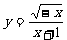 中, 自变量 x 的取值范围是( )
中, 自变量 x 的取值范围是( )
(A) x ≠-1 (B)x >-1 (C) x<0 或 x ≠-1 (D)x≤0 且x ≠-1
13 函数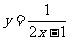 中, 自变量x 的取值范围是( )
中, 自变量x 的取值范围是( )
(A) x ≠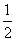 (B) x ≠ -
(B) x ≠ - 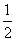 (C) x
=
(C) x
=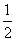 (D) x = -
(D) x = -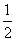
14 下列函数中, 自变量 x 的取值范围是 x ≥5 的函数是( )
(A)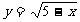 (B)
(B) 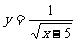 (C) y=
(C) y=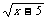 (D)
(D) 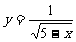
15 点A的坐标为(-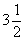 ,0),它与 x 轴上一点B的距离是
,0),它与 x 轴上一点B的距离是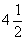 ,则B点坐标为( )
,则B点坐标为( )
(A)(1,0) (B)(- 8,0) (C)(1,0)或(-8,0)(D)以上都不对
16 在下列函数中,正比例函数是( )
(A) y = 2x+1 (B)y = 2x (C)y =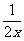 (D)y =
(D)y = 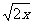
17 下列各点中,在函数y = x - 2 的图像上的点是( )
(A)(1,-1) (B)(-1,1) (C)(2,2) (D) (-2,2)
18 反比函数y = 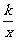 中 ,在每个象限内y 随 x 的增大而减小,则它的图像位于( )
中 ,在每个象限内y 随 x 的增大而减小,则它的图像位于( )
(A)第一,二象限(B)第二,三象限 (C) 第一,三象限 (D) 第二,四象限
19 若函数y = - x + b的图象不经过第一象限,则常数b 的取值范围是( )
(A)b>0 (B)b<0 (C)b≥0 (D)b≤0
20 若函数y = kx + b(k≠0)的图象经过第一、二、三象限,则k、b应满足( )
(A)k>0且b>0 (B)k>0且b<0(C)k<0且b>0 (D)k<0且b<0
21 一次函数y =(m-1)x + m - 1与y轴交点的纵坐标是 -1 ,则m 的值为( )(A)-1 (B)1 (C)-1,0 (D) 0
22. 抛物线y=x2-4x+1的顶点坐标是( ).
(A)(2,-3) (B)(2,3) (C)(-2,-3) (D)(-3,2)
23 点P在函数y = 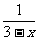 的图象上,若点P的横坐标是
的图象上,若点P的横坐标是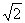 ,则点P的纵坐标为( ) (A)3 +
,则点P的纵坐标为( ) (A)3 +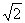 (B)3 -
(B)3 -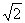 (C)
(C) 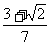 (D)
(D)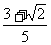
24 若函数y = kx + b的图象经过点(-1,0 )和(0,2)则k,b的值是( )
(A)k=2,b= -2 (B)k=2,b= 2 (C)k= -2,b= -2(D)k= -2,b= 2
25 函数y = x +3k 与 y = 2x - 6 的图象的交点在y 轴上,则k的值为( )
(A)3 (B)2 (C)1 (D)-2
26 已知一次函数 的图象经过一,二,三象限。则m的值为( )
的图象经过一,二,三象限。则m的值为( )
(A)m =3或m = -1 (B)m=3 (C)m=-1 (D)m=1
27 直线y = ax - 2 与直线 y = bx+1 交于x 轴上一点,则a : b 的值为( )
(A ) 2
(B)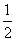 (C) -
(C) -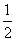 (D) -2
(D) -2
28 已知反比例函数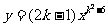 的图象的两个分支在所在的象限内,y 随x的增大而减小,那这函数的解析式为( )
的图象的两个分支在所在的象限内,y 随x的增大而减小,那这函数的解析式为( )
(A)y = -5x -1 (B) y = -5x (C) y = 3x (D)y =3x -1
29 若函数y = (3-
m)x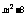 是正比例函数, 则m 的值为 ( )
是正比例函数, 则m 的值为 ( )
(A) 1 (B) ±3 (C) 3 (D) -3
31、已知抛物线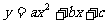 经过A(-1,0)、B(3,0)、C(0,3)三点。
经过A(-1,0)、B(3,0)、C(0,3)三点。
(1)求抛物线的解析式和顶点M的坐标,并在给定的直角坐标系中画出这条抛物线的大致图象。
(2)若点(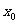 ,
,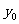 )在抛物线上,且0≤
)在抛物线上,且0≤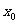 ≤4,试写出
≤4,试写出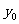 的取值范围。
的取值范围。
(3)设平行于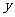 轴的直线
轴的直线 =
=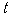 交线段BM于点P(点P能与点M重合,不能与点B重合)交
交线段BM于点P(点P能与点M重合,不能与点B重合)交 轴于点Q,四边形AQPC的面积为
轴于点Q,四边形AQPC的面积为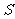 。
。
①求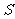 关于
关于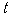 的函数关系式以及自变量
的函数关系式以及自变量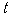 的取值范围;
的取值范围;
②求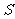 取得最大值时,点P的坐标;
取得最大值时,点P的坐标;
③设四边形OBMC的面积为 ,判断是否存在点P,使得
,判断是否存在点P,使得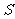 =
= ,若存在,求出点P的坐标;若不存在,请说明理由。
,若存在,求出点P的坐标;若不存在,请说明理由。

30、已知一次函数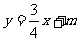 的图象分别交
的图象分别交 轴、
轴、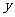 轴于A、B两点,且与反比例函数
轴于A、B两点,且与反比例函数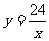 的图象在第一象限交于点C(4,
的图象在第一象限交于点C(4, ),CD⊥
),CD⊥ 轴于D。
轴于D。
(1)求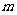 、
、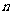 的值,并在给定的直角坐标系中作出一次函数的图象;
的值,并在给定的直角坐标系中作出一次函数的图象;
(2)如果点P、Q分别从A、C两点同时出发,以相同的速度沿线段AD、CA向D、A运动,设AP=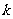 。①
。①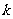 为何值时,以A、P、Q为顶点的三角形与△ADC相似?②
为何值时,以A、P、Q为顶点的三角形与△ADC相似?②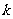 为何值时,△APQ的面积取得最大值?并求出这个最大值。
为何值时,△APQ的面积取得最大值?并求出这个最大值。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com