
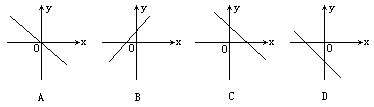
2、若一次函数y=kx+b的图象经过第一、二、四象限,则一次函数y=bx-k的图象不经过第( )象限
(A)一; (B)二; (C)三; (D)四.
1、一次函数y=-kx-k的图象大致是( )
2、通过函数的性质及定义域范围求函数的最值。
教学难点:
从实际问题中抽象概括出运动变化的规律,建立函数关系式
教学方法:讨论式教学法
教学过程:
例1、A校和B校各有旧电脑12台和6台,现决定送给C校10台、D校8台,已知从A校调一台电脑到C校、D校的费用分别是40元和80元,从B校调运一台电脑到C校、D校的运费分别是30元和50元,试求出总运费最低的调运方案,最低运费是多少?
(1)几分钟让学生认真读题,理解题意
(2)由题意可知,一种调配方案,对应一个费用。不同的调配方案对应不同的费用,在这个变化过程中,调配方案决定了总费用。它们之间存在着一定的关系。究竟是什么样的关系呢?需要我们建立数学模型,将之形式化、数学化。
解法(一)列表分析:
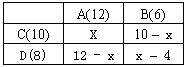
设从A校调到C校x台,则调到D校(12―x)台,B校调到C校是(10―x)台。B校调到D校是[6-(10-x)]即(x-4)台,总运费为y。
根据题意:
y = 40x+80(12- x)+ 30(10-x)+50(x-4)
y = 40x+960-80x+300-30x+50x-200
= -20x+1060(4≤x≤10,且x是正整数)
y = -20x+1060是减函数。
∴当x = 10时,y有最小值ymin= 860
∴调配方案为A校调到C校10台,调到D校2台,B校调到D校2台。
解法(二)列表分析
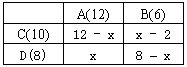
设从A校调到D校有x台,则调到C校(12―x)台。B校调到C校是[10-(12-x)]即(x-2)台。B校调到D校是(8―x)台,总运费为y。
y = 40(12 – x)+ 80x+ 30(x –2)+50(8-x)
= 480 – 40x+80x+30x – 60+400 – 50x
=20x +820(2≤x≤8,且x是正整数)
y =20x +820是增函数
∴x=2时,y有最小值ymin=860
调配方案同解法(一)
解法(三)列表分析:
解略
解法(四)列表分析:
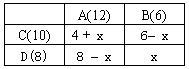
解略
例2、公司试销一种成本单价为500元/件的新产品,规定试销时的销售单价不低于成本单价,又不高于800元/件。经试销调查,发现销售量y(件),与销售单价x(元/件)可近似看作一次函数y =kx+b的关系
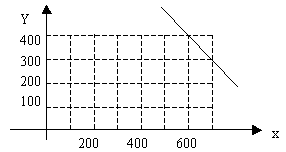
(1)根据图象,求一次函数y = kx+b的表达式
(2)设公司获得的毛利润(毛利润=销售总价―成本总价)为s元
试用销售单价x表示毛利润s;
解:如图所示
直线过点(600,400),(700,300)
∴400 = 600k+b
300 = 700k+b
k = -1,b = 1000
∴ y = - x + 1000(500≤x≤800)
s = x(1000 – x)-500(1000 – x)
=1000x – x2 – 500000 + 500x
=- x2 + 1500x – 500000(500≤x≤800)
小结:本节课试图让学生体会到函数的本质是对应关系。在实际生活中,影响事物的因素往往是多方面的,而且它们之间存在一定的关系。数学是研究现实世界的空间形式和数量关系的科学。对于实际问题我们抽象概括出它的本质特征,将其数学化、形式化,形成数学模型。这个过程既体现了数学的高度抽象性,又因其高度的抽象性决定了数学的广泛应用性。
作业:略
1、从实际问题中抽象概括出运动变化的规律,建立函数关系式。
3、能初步建立应用数学的意识,体会到数学的抽象性和广泛应用性。
教学重点:
2、渗透函数的数学思想,培养学生的数学建模能力,以及解决实际问题的能力。
1、使学生能进一步理解函数的定义,根据实际情况求函数的定义域,并能利用函数解决实际问题中的最值问题。
1、B 2、A 3、A 4、D 5、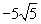 6、
6、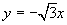 7、
7、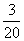 8、6 9、
8、6 9、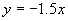 ,
,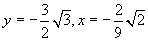 10、y=36-3t,一次函数,
10、y=36-3t,一次函数,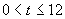 .
.
返回页首
10、拖拉机开始工作时,油箱中有油36公斤,如果每小时耗油3公斤,那么,油箱中的余油量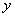 公斤与它工作的时间
公斤与它工作的时间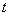 小时之间的函数关系式是什么?它是什么函数?自变量的取值范围是什么?
小时之间的函数关系式是什么?它是什么函数?自变量的取值范围是什么?
答案与提示:
9、已知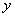 与
与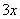 成正比例,且当
成正比例,且当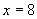 时,
时,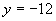
⑴求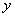 与
与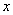 的函数解析式;
的函数解析式;
⑵求当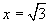 时,
时,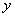 的值
的值
⑶求当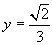 时,
时,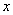 的值
的值
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com