
2.使学生知道抛物线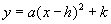 的对称轴与顶点坐标;
的对称轴与顶点坐标;
1.使学生会用描点法画出二次函数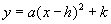 的图像;
的图像;
13.7二次函数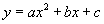 的图象(一) 的图象(一)例1: 例2: 小结: 小结: |
教材P124中1(1)、(2)
本节课学习了二次函数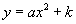 与
与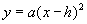 的图象的画法,主要内容如下。
的图象的画法,主要内容如下。
(出示幻灯)填写下表:(可让学生回答)
表一:
|
抛物线 |
开口方向 |
对称轴 |
顶点坐标 |
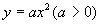 |
|
|
|
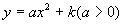 |
|
|
|
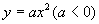 |
|
|
|
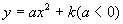 |
|
|
|
表二:
|
抛物线 |
开口方向 |
对称轴 |
顶点坐标 |
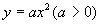 |
|
|
|
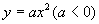 |
|
|
|
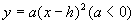 |
|
|
|
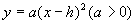 |
|
|
|
(一)函数对应值表的区别.
列表:
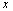 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
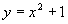 |
10 |
5 |
2 |
1 |
2 |
5 |
10 |
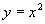 |
9 |
4 |
1 |
0 |
1 |
4 |
7 |
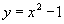 |
8 |
3 |
0 |
-1 |
0 |
3 |
8 |
列完表之后,让学生观察上表归纳出,对于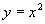 与
与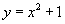 ,任意一个
,任意一个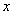 的值,解析式
的值,解析式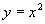 的函数值总比
的函数值总比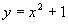 的函数值小1,对于同一个
的函数值小1,对于同一个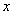 值,
值,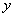 值总是小1,抛物线上的点向下平行移动一个单位,图象也向下平移一个单位.对于
值总是小1,抛物线上的点向下平行移动一个单位,图象也向下平移一个单位.对于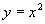 与
与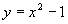 也这样分析.分析完表后,再让同学们看课件中画出的函数
也这样分析.分析完表后,再让同学们看课件中画出的函数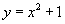 与
与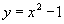 的图象.
的图象.
复习提问:用描点法画出函数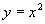 的图象,并根据图象指出:抛物线
的图象,并根据图象指出:抛物线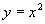 的开口方向,对称轴与顶点坐标.(插入
的开口方向,对称轴与顶点坐标.(插入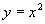 的图片)
的图片)
教师可边提问边打开图片,然后可以找学生来指出抛物线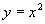 的开口方向,对称轴及顶点坐标,针对学生的回答情况加以总结,评价.
的开口方向,对称轴及顶点坐标,针对学生的回答情况加以总结,评价.
下面,我们来看一下如何完成下面的例题?
例1 在同一平面直角坐标系画出函数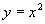 、
、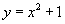 、
、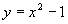 的图象.(插入课件)
的图象.(插入课件)
3.形如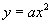 的二次函数的开口方向,对称轴,顶点坐标各是什么?
的二次函数的开口方向,对称轴,顶点坐标各是什么?
通过这三个问题,进一步复习巩固所学的知识点,同时引出本节课要学习的问题.
从这节课开始,我们就来研究二次函数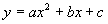 的图象.(板书课题)
的图象.(板书课题)
提问:1.什么是二次函数?
2.我们已研究过了什么样的二次函数?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com