
3、分别指出下列各关系式中的变量与常量:
(1)球的表面积S(cm2)与球半径R(cm)的关系式是S=4πR2;
(2)设圆柱的底面半径R(cm)不变,圆柱的体积V(m3)与圆柱的高h(m)的关系式是v=πR2h;
(3)以固定的速度VO(米/秒)向上抛一个小球,小球的高度h(米)与小球运动的时间t(秒)之间的关系式是h=VOt-4.9t2.
2、填空
(1)平行四边形相邻的边长为x、y,它的周长是30,则y关于x的函数关系式是_______,自变量x的取值范围是____________________.
(2)某水果批发市场规定,批发水果不少于100千克时,批发价为每千克2.5元.小于携带现金3000元到市场采购苹果,并以批发价买进,如果购买的苹果为x千克,小王付款后的剩余现金为y元,则y与x之间的函数关系式是___,自变量x的取值范围是__________.
(3)用50牛的力推动一个物体,所做的功W(焦)与物体移动距离S(米)之间的函数关系式是________,自变量S的取值范围是__________.
1、选择题
(1)在△ABC中,它的底边长是a,底边上的高是h,则三角形面积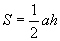 ,当a为定长时,在此式子中(
)
,当a为定长时,在此式子中(
)
(A)S、h是变量,a是常量 (B)S、h、a是变量, 是常量
是常量
(C)a、h是变量, 、S是常量 (D)S是变量,
、S是常量 (D)S是变量, 、a、h是常量
、a、h是常量
(2)在函数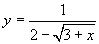 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )
(A)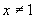 (B)
(B)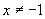
(C) 且
且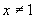 (D)
(D) 或
或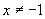
(3)已知函数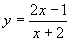 ,当
,当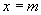 时函数值为1,则m值为( )
时函数值为1,则m值为( )
(A)1 (B)3 (C)-3 (D)-1
(4)若函数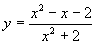 ,与函数值
,与函数值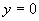 对应的x的值是( )
对应的x的值是( )
(A)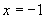 或
或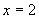 (B)
(B)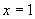 或
或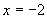
(C)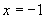 且
且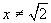 (D)
(D)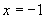 或
或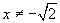
(5)自变量的取值范围是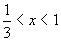 的函数是( )
的函数是( )
(A)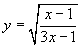 (B)
(B)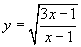
(C)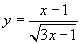 (D)
(D)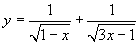
教材P114 1、2、3
(二)总结、扩展
教师提问,学生思考回答:
1.你能否说清二次函数的意义?
注意总结:(1)函数解析式关于自变量是整式;(2)自变量的最高次数是2。
2.二次函数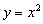 的图像是什么形状的?它的开口方向,对称轴,顶点坐标各是什么?
的图像是什么形状的?它的开口方向,对称轴,顶点坐标各是什么?
(一)教学过程
首先,我们来看两个实验问题:(出示幻灯)
1.圆的半径是R,它的面积为S,你能否写出S与R之间的函数关系式?
这个问题由学生举手回答,可找层次较低的学生完成,培养他们的参与意识和自信心。然后把答案写在黑板上留用。
2.已知一个矩形场地的周长是60,一边长为l,请你写出这个矩形场地的面积S与这条边长之间的函数关系式。
这个问题其实就是13.2中的例1,可由学生得出结论,若学生给出的是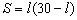 ,再继续提问:你能否把函数关系式中的括号去掉?然后把所得的结论写在黑板上。
,再继续提问:你能否把函数关系式中的括号去掉?然后把所得的结论写在黑板上。
提问:比较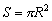 与
与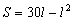 这两个函数,都是用自变量的几次式来表示的?
这两个函数,都是用自变量的几次式来表示的?
用这个问题,引出二次函数,在学生回答之后,教师加以总结,板书:
一般地,如果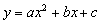 (a、b、c是常数,
(a、b、c是常数,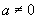 ),那么,y叫做x的二次函数。
),那么,y叫做x的二次函数。
提问:1.上述概念中的a为什么不能是0?
2.对于二次函数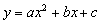 中的b和c可否为0?若b和c其一为0或均为0,上述函数的式子可以改写成怎样?你认为它们还是不是二次函数?
中的b和c可否为0?若b和c其一为0或均为0,上述函数的式子可以改写成怎样?你认为它们还是不是二次函数?
3.由问题1和2,你能否总结:一个函数是否是二次函数,关键看什么?
由这三个问题加深学生对二次函数意义的理解,也同时给出了二次函数的三个特例: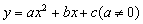 ;
;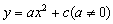 ;
;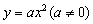 ,使学生深刻理解:看一个函数是否是二次函数的关键是看二次项的系数是否为0.
,使学生深刻理解:看一个函数是否是二次函数的关键是看二次项的系数是否为0.
4.二次函数的解析式,与我们所学过的什么知识相类似?
通过这个问题,使学生能把二次函数与一元二次方程初步搭上联系即可,为以后的教学
做好铺垫.
练习一:P108中1、2 口答,注意第1题要让学生说明不是二次函数的原因
提问:根据我们所学知道,一次函数的图像是条直线,那么二次函数的图像又是什么样的呢?
这个问题主要是为了引起学生的兴趣,不必回答,教师也不用给出答案.
我们研究任何问题都最好由最简单的入手,根据刚才对二次函数的介绍,你认为最简单的二次函数是什么?
这个问题一方面可以使学生自然过渡到要先研究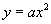 .另一方面也使同学认识到研
.另一方面也使同学认识到研
究问题要由简到繁的基本方法.
所以第三个问题是,由我们学习的画函数的图像方法与步骤,我们应怎样画二次函数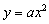 的图像呢?
的图像呢?
可由学生先回答画函数图像的三个步骤:(1)列表;(2)描点;(3)连线.然后分步骤来研究这个图像的方法.
(1)列表:①自变量x的取值范围是什么?
②要画这个图,你认为x取整数还是取其他数较好?
③看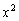 ,它是一个数的平方形式,它的结论与x的值有什么关系?
,它是一个数的平方形式,它的结论与x的值有什么关系?
学生可能有多种答法,引导学生回答:当x取互为相反数时,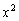 的值相同.
的值相同.
④若选7个点画图,你准备怎样选?
通过这4个问题可以使学生很顺利地想到为什么要先取书上给出的这7个点,而且也使
学生初步学会画二次函数图像时选点的技巧.
(2)描点:①在画坐标系时x轴的正、负半铀和y轴的正、负半轴是否都要画一样的长?
②怎样画就可以了呢?
答:x轴的正、负半轴画的一样长,y的正半轴画的较长,负半轴画的较短就可以.
通过这两个问题可培养学生的作图技巧.
(2)连线:①观察这7个点的位置,它们是否在一条直线上?
②我们应怎样连接这7个点?
让学生先连一次试试,然后教师演示。关于原点附近的变化趋势,最好能用动画演示,增强学生的直观认识,或看书也可以.
注意:我们所画的只是近似图像.
接下来,让学生观察这个函数图像提问:
1.函数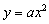 的图像有什么特点?
的图像有什么特点?
答:是轴对称图形.
2.你是怎样判断函数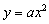 的图像有上述特征的?
的图像有上述特征的?
这个问题,按不同的层次,有三种得出方法:(1)观察图;(2)看列表;(3)直接根据解析式,看学生层次定讲解的深度.
学生回答完上面的问题之后就可指出:函数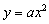 的图像是一条关于y轴对称的曲线,这条曲线叫做抛物线。实际上,二次函数的图像都是抛物线(板书)
的图像是一条关于y轴对称的曲线,这条曲线叫做抛物线。实际上,二次函数的图像都是抛物线(板书)
在此处,可大致解释一下抛物线是由物理中的问题而来的,不要深讲。
再结合图像指出:抛物线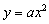 是开口向上的,y轴是它的对称轴,对称轴与抛物线的交点是抛物线的顶点,即(0,0)点。
是开口向上的,y轴是它的对称轴,对称轴与抛物线的交点是抛物线的顶点,即(0,0)点。
关于抛物线的顶点,可按不同层次的学生进行不同层次的解释:
从图像上直观得到:抛物线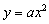 的顶点是图像的最低点:从解析式上看,当
的顶点是图像的最低点:从解析式上看,当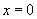 时,
时,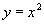 取得最小值0,(0,0)就是抛物线
取得最小值0,(0,0)就是抛物线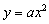 的顶点坐标。
的顶点坐标。
4.解决办法:(1)关于二次函数的定义,关键要注意:自变量的最高次数定义,二次项系数 ;(2)
;(2)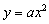 的图像和性质,不可死记硬背,要结合图像理解和掌握二次函数
的图像和性质,不可死记硬背,要结合图像理解和掌握二次函数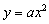 的几个主要特征,如开口方向,顶点坐标(或位置),对称轴,最大值最小值等。
的几个主要特征,如开口方向,顶点坐标(或位置),对称轴,最大值最小值等。
3.教学疑点:(1)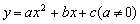 ;(2)
;(2) 的图像的反性质。
的图像的反性质。
2.教学难点:正确画出二次函数 的图像。因为它的图像是一条曲线,画起来较复杂,而且学生在画图之前,尚不清楚二次函数
的图像。因为它的图像是一条曲线,画起来较复杂,而且学生在画图之前,尚不清楚二次函数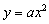 的图像的具体形状和变化趋势,所以不易把握。
的图像的具体形状和变化趋势,所以不易把握。
1.教学重点:二次函数的意义及二次函数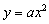 的图像的画法。因为它们是研究二次函数的重要基础。
的图像的画法。因为它们是研究二次函数的重要基础。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com