
2、在识图过程中,渗透数形结合的数学思想.
1、培养学生看图识图的能力.
这节课,我们进一步地研究了有关函数的概念.在研究函数关系时首先要考虑自变量的取值范围.因此,要求大家能掌握解析式含有一个自变量的简单的整式、分式、二次根式的函数的自变量取值范围的求法,并能求出其相应的函数值.另外,对于反映实际问题的函数关系,要具体问题具体分析.
作业:习题13.2A组2、3、5
刚才所举例子中的函数,都是利用数学式子即解析式表示的.这种用数学式子表示函数时,要考虑自变量的取值必须使解析式有意义.如第一题中的学生数n必须是正整数.
例1、求下列函数中自变量x的取值范围.
(1)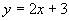 (2)
(2)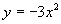
(3)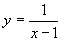 (4)
(4)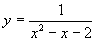
(5)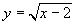 (6)
(6)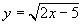
分析:在(1)、(2)中,x取任意实数,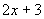 与
与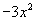 都有意义.
都有意义.
(3)小题的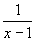 是一个分式,分式成立的条件是分母不为0.这道题的分母是
是一个分式,分式成立的条件是分母不为0.这道题的分母是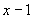 ,因此要求
,因此要求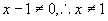 .
.
同理(4)小题的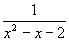 也是分式,分式成立的条件是分母不为0,这道题的分母是
也是分式,分式成立的条件是分母不为0,这道题的分母是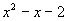 ,因此要求
,因此要求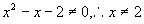 且
且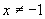 .
.
第(5)小题,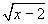 是二次根式,二次根式成立的条件是被开方数大于、等于零.
是二次根式,二次根式成立的条件是被开方数大于、等于零.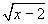 的被开方数是
的被开方数是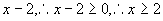 .
.
同理,第(6)小题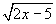 也是二次根式,
也是二次根式,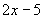 是被开方数,
是被开方数,
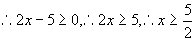 .
.
解:(1)全体实数
(2)全体实数
(3)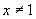
(4) 且
且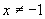
(5)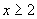
(6)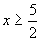
小结:从上面的例题中可以看出函数的解析式是整数时,自变量可取全体实数;函数的解析式是分式时,自变量的取值应使分母不为零;函数的解析式是二次根式时,自变量的取值应使被开方数大于、等于零.
注意:有些同学没有真正理解解析式是分式时,自变量的取值应使分母不为零,片面地认为,凡是分母,只要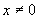 即可.教师可将解题步骤设计得细致一些.先提问本题的分母是什么?然后再要求分式的分母不为零.求出使函数成立的自变量的取值范围.二次根式的问题也与次类似.
即可.教师可将解题步骤设计得细致一些.先提问本题的分母是什么?然后再要求分式的分母不为零.求出使函数成立的自变量的取值范围.二次根式的问题也与次类似.
但象第(4)小题,有些同学会犯这样的错误,将答案写成 或
或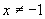 .在解一元二次方程时,方程的两根用“或者”联接,在这里就直接拿过来用.限于初中学生的接受能力,教师可联系日常生活讲清“且”与“或”.说明这里
.在解一元二次方程时,方程的两根用“或者”联接,在这里就直接拿过来用.限于初中学生的接受能力,教师可联系日常生活讲清“且”与“或”.说明这里 与
与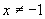 是并且的关系.即2与-1这两个值x都不能取.
是并且的关系.即2与-1这两个值x都不能取.
例2、自行车保管站在某个星期日保管的自行车共有3500辆次,其中变速车保管费是每辆一次0.5元,一般车保管费是每次一辆0.3元.
(1)若设一般车停放的辆次数为x,总的保管费收入为y元,试写出y关于x的函数关系式;
(2)若估计前来停放的3500辆次自行车中,变速车的辆次不小于25%,但不大于40%,试求该保管站这个星期日收入保管费总数的范围.
解:(1)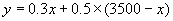
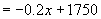 (x是正整数,
(x是正整数,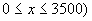
(2)若变速车的辆次不小于25%,但不大于40%,
则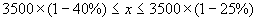
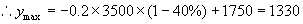
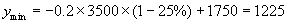
收入在1225元至1330元之间
总结:对于反映实际问题的函数关系,应使得实际问题有意义.这样,就要求联系实际,具体问题具体分析.
对于函数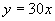 ,当自变量
,当自变量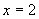 时,相应的函数y的值是
时,相应的函数y的值是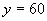 .60叫做这个函数当
.60叫做这个函数当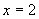 时的函数值.
时的函数值.
例3、求下列函数当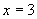 时的函数值:
时的函数值:
(1)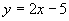 (2)
(2)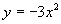
(3)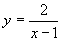 (4)
(4)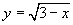
解:1)当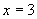 时,
时,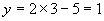
(2)当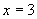 时,
时,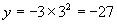
(3)当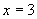 时,
时,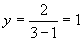
(4)当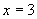 时,
时,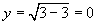
注:本例既锻炼了学生的计算能力,又创设了情境,让学生体会对于x的每一个值,y都有唯一确定的值与之对应.以此加深对函数的理解.
2、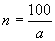 ,n是函数,a是自变量.
,n是函数,a是自变量.
2、为迎接新年,班委会计划购买100元的小礼物送给同学,求所能购买的总数n(个)与单价(a)元的关系.
解:1、y=30n
y是函数,n是自变量
上一节课我们讲了函数的概念:一般地,设在一个变化过程中有两个变量x、y,如果对于x的每一个值,y都有唯一的值与它对应,那么就说x是自变量,y是x的函数.
生活中有很多实例反映了函数关系,你能举出一个,并指出式中的自变量与函数吗?
1、学校计划组织一次春游,学生每人交30元,求总金额y(元)与学生数n(个)的关系.
6、设某种电报收费标准是每个字0.1元,写出电报费y(元)与字数x(个)之间的函数关系式,并求自变量x的取值范围.
5、求下列函数中,自变量x的取值范围;
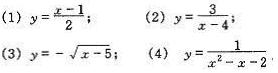
4、分别写出下列函数关系式,并指出式中的自变量与函数:
(1)设一长方体盒子高为10cm,底面是正方形,求这个长方体的体积V(cm3)与底面边长a(cm)的关系;
(2)秀水村的耕地面积是106(m2),求这个村人均占有耕地面积x(m2)与人数n的关系
(3)设地面气温是20℃,如果每升高1km,气温下降6℃,求气温t(℃)与高度h(km)的关系.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com