
1.教学重点:反比例的概念、图像、性质以及用待定系数法确定反比例函数的解析式.因为要研究反比例函数就必须明确反比例函数的上述问题.
教师采用类比法、观察法、练习法
学生学习反比例函数要与学习其他函数一样,要善于数形结合,由解析式联想到图像的位置及其性质,由图像和性质联想比例系数k的符号.
(四)美育渗透点
通过反比例函数图像的研究,渗透反映其性质的图像的直观形象美,激发学生的兴趣,也培养学生积极探求知识的能力.
(三)德育渗透点
1.向学生渗透数学来源于实践又反过来作用于实践的观点;
2.使学生体会事物是有规律地变化着的观点.
(二)能力训练点
1.培养学生的作图、观察、分析、总结的能力;
2.向学生渗透数形结合的教学思想方法.
(一)知识教学点
1.使学生了解反比例函数的概念;
2.使学生能够根据问题中的条件确定反比例函数的解析式;
3.使学生理解反比例函数的性质,会画出它们的图像,以及根据图像指出函数值随自变量的增加或减小而变化的情况;
4.会用待定系数法确定反比例函数的解析式.
5、布置作业 习题13.8 1-4
3、观察图象,归纳、总结出反比例函数的性质
前面学习了三类基本的初等函数,有了一定的基础,这里可视学生的程度或展开全面的讨论,或在老师的引导下完成知识的学习.
显示这两个函数的图象,提出问题:你能从图象上发现什么有关反比例函数的性质呢?并能从解析式或列表中得到论证.(下列答案仅供参考)
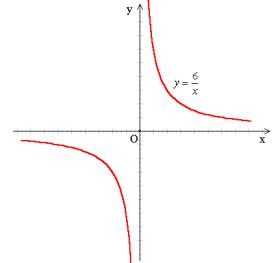
(1)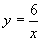 的图象在第一、三象限.可以扩展到k >0时的情形,即k>0时,双曲线两支各在第一和第三象限.从解析式中,也可以得出这个结论:xy=k,即x与y同号,因此,图象在第一、三象限.
的图象在第一、三象限.可以扩展到k >0时的情形,即k>0时,双曲线两支各在第一和第三象限.从解析式中,也可以得出这个结论:xy=k,即x与y同号,因此,图象在第一、三象限.
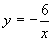 的讨论与此类似.
抓住机会,说明数与形的统一,也渗透了数形结合的数学思想方法.体现了由特殊到一般的研究过程.
(2)函数
的讨论与此类似.
抓住机会,说明数与形的统一,也渗透了数形结合的数学思想方法.体现了由特殊到一般的研究过程.
(2)函数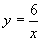 的图象,在每一个象限内,y随x的增大而减小;
从图象中可以看出,当x从左向右变化时,图象呈下坡趋势.从列表中也可以看出这样的变化趋势.有理数除法说明了同样的道理,被除数一定时,若除数大于零,除数越大,商越小;若除数小于零,同样是除数越大,商越小.由此可归纳出,当k>0时,函数
的图象,在每一个象限内,y随x的增大而减小;
从图象中可以看出,当x从左向右变化时,图象呈下坡趋势.从列表中也可以看出这样的变化趋势.有理数除法说明了同样的道理,被除数一定时,若除数大于零,除数越大,商越小;若除数小于零,同样是除数越大,商越小.由此可归纳出,当k>0时,函数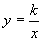 的图象,在每一个象限内,y随x的增大而减小.
同样可以推出
的图象,在每一个象限内,y随x的增大而减小.
同样可以推出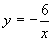 的图象的性质.
(3)函数
的图象的性质.
(3)函数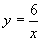 的图象不经过原点,且不与x轴、y轴交.从解析式中也可以看出,
的图象不经过原点,且不与x轴、y轴交.从解析式中也可以看出, .如果x取值越来越大时,y的值越来越小,趋近于零;如果x取负值且越来越小时,y的值也越来越趋近于零.因此,呈现的是双曲线的样子.同理,抽象出
.如果x取值越来越大时,y的值越来越小,趋近于零;如果x取负值且越来越小时,y的值也越来越趋近于零.因此,呈现的是双曲线的样子.同理,抽象出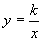 图象的性质.
函数
图象的性质.
函数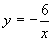 的图象性质的讨论与次类似.
4、小结:
的图象性质的讨论与次类似.
4、小结:
本节课我们学习了反比例函数的概念及其图象的性质.大家展开了充分的讨论,对函数的概念,函数的图象的性质有了进一步的认识.数学学习要求我们要深刻地理解,找出事物间的普遍联系和发展规律,能数学地发现问题,并能运用已有的数学知识,给以一定的解释.即数学是世界的一个部分,同时又隐藏在世界中.
2、列表、描点画出反比例函数的图象
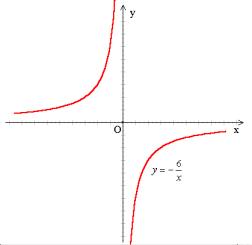
例1、画出反比例函数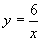 与
与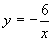 的图象
解:列表
的图象
解:列表
|
x |
-6 |
-5 |
-4 |
-3 |
1 |
2 |
3 |
4 |
5 |
6 |
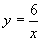 |
-1 |
-1.2 |
-1.5 |
-2 |
6 |
3 |
2 |
1.5 |
1.2 |
1 |
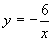 |
1 |
1.2 |
1.5 |
2 |
-6 |
-3 |
-2 |
-1.5 |
-1.2 |
1 |
说明:由于学生第一次接触反比例函数,无法推测出它的大致图象.取点的时候最好多取几个,正负可以对称着取分别画点描图
一般地反比例函数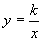 (k是常数,
(k是常数,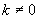 )的图象由两条曲线组成,叫做双曲线.
)的图象由两条曲线组成,叫做双曲线.
1、从实际引出反比例函数的概念
我们在小学学过反比例关系.例如:当路程S一定时,时间t与速度v成反比例
即vt=S(S是常数);
当矩形面积S一定时,长a与宽b成反比例,即ab=S(S是常数)
从函数的观点看,在运动变化的过程中,有两个变量可以分别看成自变量与函数,写成:
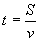 (S是常数)
(S是常数)
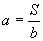 (S是常数)
一般地,函数
(S是常数)
一般地,函数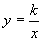 (k是常数,
(k是常数,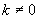 )叫做反比例函数.
)叫做反比例函数.
如上例,当路程S是常数时,时间t就是v的反比例函数.当矩形面积S是常数时,长a是宽b的反比例函数.
在现实生活中,也有许多反比例关系的例子.可以组织学生进行讨论.下面的例子仅供
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com