
2、填空题
(1)坐标平面内的点与________是一一对应的;
(2)点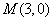 到点
到点 的距离是________;
的距离是________;
(3)点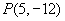 到原点的距离是________;
到原点的距离是________;
(4)点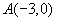 在________上;
在________上;
(5)点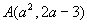 在第二、第四象限坐标轴夹角平分线上,那么
在第二、第四象限坐标轴夹角平分线上,那么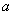 =________;
=________;
(6)设点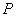 的坐标为
的坐标为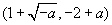 ,则点
,则点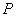 在第________象限;
在第________象限;
(7)已知点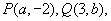 且
且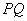 ∥
∥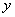 轴,则
轴,则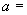 ________,
________,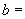 ________.
________.
(8)点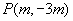 是第二象限内的点,则
是第二象限内的点,则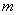 的取值范围是________.
的取值范围是________.
(9)以点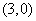 为圆心,5为半径的圆与
为圆心,5为半径的圆与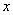 轴的两个交点分别为________,与
轴的两个交点分别为________,与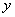 轴的两个交点分别为________.
轴的两个交点分别为________.
1、选择题
(1)点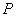 位于
位于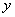 轴左方,距
轴左方,距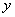 轴3个单位长,位于( )
轴3个单位长,位于( )
A、(3,-4) B、(-3,4) C、(4,-3) D、(-4,3)
(2)如果点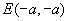 在第一象限,那么点
在第一象限,那么点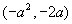 在( )
在( )
A、第四象限 B、第三象限 C、第二象限 D、第一象限
(3)点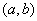 关于
关于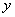 轴的对称点的坐标是( )
轴的对称点的坐标是( )
A、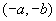 B、
B、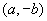 C、
C、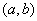 D、
D、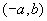
(4)矩形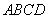 中,三点的坐标分别是
中,三点的坐标分别是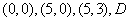 点的坐标是( )
点的坐标是( )
A、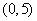 B、
B、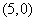 C、
C、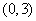 D、
D、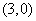
(5)已知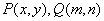 ,如果
,如果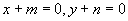 ,那么点
,那么点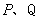 ( )
( )
A、关于原点对称 B、关于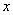 轴对称
轴对称
C、关于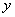 轴对称 D、关于过点
轴对称 D、关于过点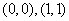 的直线对称
的直线对称
(6)直角坐标系中有一点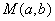 ,其中
,其中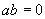 ,则点
,则点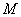 的位置在( )
的位置在( )
A、原点 B、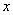 轴上 C、
轴上 C、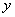 轴上 D、坐标轴上
轴上 D、坐标轴上
(7)直角坐标系中,点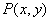 在第二象限,且
在第二象限,且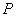 到
到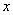 轴、
轴、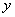 轴距离分别为3,7,则
轴距离分别为3,7,则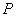 点坐标为( )
点坐标为( )
A、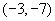 B、
B、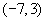 C、
C、 D、
D、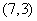
|
13.8反比例函数及其图像 引例:(1)例1 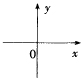 : 例2: 例3: : 例2: 例3:(2) 1.反比例函数: 2.反比例函数的性质 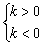 |
2.选做:P130中B1,2
1.教材P130中4,5,6
(二)总结、扩展
教师提问,学生思考回答:
1.什么是反比例函数?
2.反比例函数的图像是什么样的?
3.反比例函数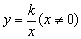 的性质是什么?
的性质是什么?
4.命题方向及题型设置,反比例函数也是中考命题的主要考点,其图像和性质,以及其函数解析式的确定,常以填空题、选择题出现,在低档题中,近两年各省、市的中考试卷中出现不少将反比例函数与一次函数、几何知识、三角知识等综合编拟的解答题,丰富了压轴题的形式和内容.
(一)教学过程
提问:小学是否学过反比例关系?是如何叙述的?
由学生先考虑及讨论一下.
答:小学学过:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做反比例的量,它们的关系叫做反比例关系.
看下面的实例:(出示幻灯)
1. 当路程s一定时,时间t与速度v成反比例;
2.当矩形面积S一定时,长a与宽b成反比例;
它们分别可以写成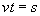 (s是常数),
(s是常数),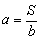 (S是常数)写在黑板上,用以得出反比例函数的概念:(板书)
(S是常数)写在黑板上,用以得出反比例函数的概念:(板书)
一般地,函数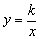 (k是常数,
(k是常数,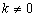 )叫做反比例函数.
)叫做反比例函数.
即在上面的例子中,当路程s是常数时,时间t就是速度v的反比例函数,能否说:速度v是时间t的反比例函数呢?
通过这个问题,使学生进一步理解反比例函数的概念,只要满足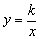 (k是常数,
(k是常数,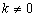 )就可以.因此可以说速度v是时间t的反比例函数,因为
)就可以.因此可以说速度v是时间t的反比例函数,因为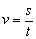 (s是常量).对第2个实例也一样.
(s是常量).对第2个实例也一样.
练习一:教材P129中1 口答.P130 1
根据前面学习特殊函数的经验,研究完函数的概念,跟着要研究的是什么?
答:图像和性质.
通过这个问题,使学生对课本上给出的知识的发生、发展过程有一个明确的认识,以后
学生要研究其他函数,也可以按照这种方式来研究.
下面,我们就来看一个例题:(出示幻灯)
例1 画出反比例函数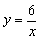 与
与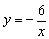 的图像.
的图像.
提问:1.画函数图像的关键问题是什么?
答:合理、正确地选值列表.
2.在选值时,你认为要注意什么问题?
答:(1)由于函数图像的特点还不清楚,多选几个点较好;
(2)不能选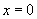 ,因为
,因为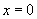 时函数无意义;
时函数无意义;
(3)选整数较好计算和描点.
这个问题中最核心的一点是关于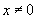 的问题,提醒学生注意.
的问题,提醒学生注意.
3.你能不能自己完成这道题呢?
学生在练习本上列表、描点、连线,教师在黑板上板演,到连线时可暂停,让学生先连完线之后,找一名同学上黑板连线,然后就这名同学的连线加以评价、总结:
注意:(1)一般地,反比例函数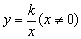 的图像由两条曲线组成,叫做双曲线;
的图像由两条曲线组成,叫做双曲线;
(2)这两条曲线不相交;
(3)这两条曲线无限延伸,无限靠近x轴和y轴,但永不会与x轴和y轴相交.
关于注意(3)可问学生:为什么图像与x和y轴不相交?
通过这个问题既可加深学生对反比例函数图像的记忆,又可培养学生思维的灵活性和深刻性.
再让学生观察黑板上的图,提问:
1.当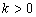 时,双曲线的两个分支各在哪个象限?在每个象限内,y随x的增大怎样变化?
时,双曲线的两个分支各在哪个象限?在每个象限内,y随x的增大怎样变化?
2.当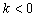 时,双曲线的两个分支各在哪个象限?在每个象限内,y随x的增大怎样变化?
时,双曲线的两个分支各在哪个象限?在每个象限内,y随x的增大怎样变化?
这两个问题由学生讨论总结之后回答,教师板书:
对于双曲线(1)当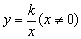 :(1)当
:(1)当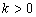 时,双曲线的两分支位于一、三象限,y随x的增大而减少;(2)当
时,双曲线的两分支位于一、三象限,y随x的增大而减少;(2)当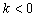 时,双曲线的两分支位于二、四象限,y随x的增大而增大.
时,双曲线的两分支位于二、四象限,y随x的增大而增大.
3.反比例函数的这一性质与正比例函数的性质有何异同?
通过这个问题使学生能把学过的相关知识有机地串联起来,便于记忆和应用.
练习二:教材P129中2由学生在练习本上完成,教师巡回指导.P130中2、3填在书上
上面,我们讨论了反比例函数的概念、图像和性质,下面我们再来看一个不同类型的例题:(出示幻灯)
例2已知y与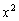 成反比例,并且当
成反比例,并且当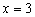 时,
时,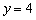 ,求
,求 时,y的值.
时,y的值.
用提问的方式对此题加以分析:
(1)y与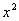 成反比例是什么含义?
成反比例是什么含义?
由学生讨论这一问题,最后归结为根据反比例函数的概念,这句话说明了: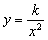 .
.
(2)根据这个式子,能否求出当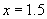 时,y的值?
时,y的值?
(3)要想求出y的值,必须先知道哪个量呢?
(4)怎样才能确定k的值?用什么条件?
答:用待定系数法,把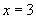 时
时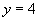 代入
代入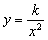 ,求出k的值.
,求出k的值.
(5)你能否自己完成这道例题:
由一名同学板演,其他同学在练习本上完成.
例3 已知: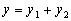 ,
,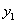 与x成正比例,
与x成正比例,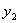 与x成反比例,当
与x成反比例,当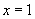 时,
时,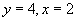 时,
时, ,求y与x的解析式.
,求y与x的解析式.
分析:一定要先写出y与x的函数表达式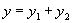 ,
,
要用x分别把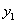 ,
,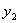 表示出来得
表示出来得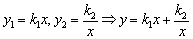 ,
,
要注意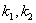 不能写成k,∴
不能写成k,∴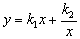
解:设 ,
,
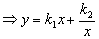 .
.
由题意得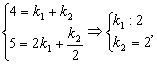
∴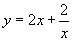 .
.
4.解决办法:(1)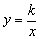 中隐含条件是
中隐含条件是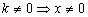 或
或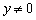 ;(2)双曲线的两个分支是断开的,研究函数的增减性时,要将两个分支分别讨论,不能一概而论.
;(2)双曲线的两个分支是断开的,研究函数的增减性时,要将两个分支分别讨论,不能一概而论.
3.教学疑点:(1)反比例函数为何与x轴,y轴无交点;(2)反比例函数的图像只能说在第一、三象限或第二、四象限,而不能说经过第几象限,增减性也要说明在第几象限(或说在它的每一个象限内).
2.教学难点:画反比例函数的图像.因为反比例函数的图像有两个分支,而且这两个分支的变化趋势又不同,学生初次接触,一定会感到困难.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com