2、培养学生观察、理解能力，综合运用知识分析问题和解决问题的能力；

圆、扇形、弓形的面积(二)

　教学目标：

1、在复习巩固圆面积、扇形面积的计算的基础上，会计算弓形面积；

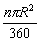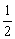　知识：扇形及扇形面积公式S_扇形= ，S_扇形= lR．

　方法能力：迁移能力，对比方法；计算能力的培养．

5、已知半径为2的扇形，面积为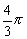 ，则这个扇形的弧长=____．

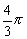　( ，2，120°， ， )

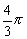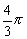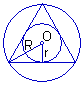　例1、已知正三角形的边长为a，求它的内切圆与外接圆组成的圆环的面积．

　学生独立完成，对基础较差的学生教师指导

　(1)怎样求圆环的面积？

　(2)如果设外接圆的半径为R，内切圆的半径为r， R、r与已知边长a有什么联系？

　解：设正三角形的外接圆、内切圆的半径分别为R，r，面积为S₁、S₂．

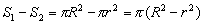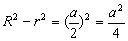　S= ．

　∵ ，∴S= ．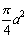

　说明：要注意整体代入．

　对于教材中的例2，可以采用典型例题中第4题，充分让学生探究．

　课堂练习：教材P181练习中2、4题．

4、已知半径为2cm的扇形，其弧长为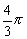 ，则这个扇形的面积，S_扇=____．

3、已知半径为2的扇形，面积为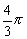 ，则它的圆心角的度数=____．

　练习：1、已知扇形的圆心角为120°，半径为2，则这个扇形的面积，S_扇=____．

2、已知扇形面积为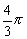 ，圆心角为120°，则这个扇形的半径R=____．

　教师引导学生理解：

　(1)在应用扇形的面积公式S_扇形=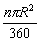 进行计算时，要注意公式中n的意义．n表示1°圆心角的倍数，它是不带单位的；

　(2)公式可以理解记忆(即按照上面推导过程记忆)；

　提出问题：扇形的面积公式与弧长公式有联系吗？(教师组织学生探讨)

S_扇形=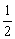 lR

　想一想：这个公式与什么公式类似？(教师引导学生进行，或小组协作研究)

　与三角形的面积公式类似，只要把扇形看成一个曲边三角形，把弧长l看作底，R看作高就行了．这样对比，帮助学生记忆公式．实际上，把扇形的弧分得越来越小，作经过各分点的半径，并顺次连结各分点，得到越来越多的小三角形，那么扇形的面积就是这些小三角形面积和的极限．要让学生在理解的基础上记住公式．

2、探究新问题

　教师组织学生对比研究：

　(1)圆面积S=πR²；

　(2)圆心角为1°的扇形的面积= ；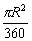

　(3)圆心角为n°的扇形的面积是圆心角为1°的扇形的面积n倍；

　(4)圆心角为n°的扇形的面积= ．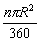

　归纳结论：若设⊙O半径为R，圆心角为n°的扇形的面积S_扇形，则

S_扇形=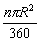 (扇形面积公式)

1、迁移方法

　教师引导学生迁移推导弧长公式的方法步骤：

　(1)圆周长C=2πR；

　(2)1°圆心角所对弧长= ；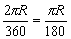

　(3)n°圆心角所对的弧长是1°圆心角所对的弧长的n倍；

　(4)n°圆心角所对弧长= ．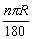

　归纳结论：若设⊙O半径为R， n°圆心角所对弧长l，则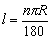 　 (弧长公式)