
知识:(1)正多边形的概念.(2)n等分圆周(n≥3)可得圆的内接正n边形和圆的外切正n边形.
能力和方法:正多边形的证明方法和思路,正多边形判断能力
3.如图,已知点A、B、C、D、E是⊙O的5等分点,画出⊙O的内接和外切正五边形.
2.求证:正五边形的对角线相等.
P157练习
1、(口答)矩形是正多边形吗?菱形是正多边形吗?为什么?
定理:把圆分成n(n≥3)等份:
(1)依次连结各分点所得的多边形是这个圆的内接正n边形;
(2)经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形.
我们以n=5的情况进行证明.
已知:⊙O中, 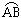 =
= 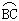 =
= 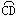 =
= 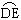 =
=  ,TP、PQ、QR、RS、ST分别是经过点A、B、C、D、E的⊙O的切线.
,TP、PQ、QR、RS、ST分别是经过点A、B、C、D、E的⊙O的切线.
求证:(1)五边形ABCDE是⊙O的内接正五边形;
(2)五边形PQRST是⊙O的外切正五边形.
证明:(略)
引导学生分析、归纳证明思路:
弧相等
说明:(1)要判定一个多边形是不是正多边形,除根据定义来判定外,还可以根据这个定理来判定,即:①依次连结圆的n(n≥3)等分点,所得的多边形是正多迫形;②经过圆的n(n≥3)等分点作圆的切线,相邻切线相交成的多边形是正多边形.
(2)要注意定理中的“依次”、“相邻”等条件.
(3)此定理被称为正多边形的判定定理,我们可以根据它判断一多边形为正多边形或根据它作正多边形.
(1)概念:各边相等、各角也相等的多边形叫做正多边形.如果一个正多边形有n(n≥3)条边,就叫正n边形.等边三角形有三条边叫正三角形,正方形有四条边叫正四边形.
(2)概念理解:
①请同学们举例,自己在日常生活中见过的正多边形.(正三角形、正方形、正六边形,…….)
②矩形是正多边形吗?为什么?菱形是正多边形吗?为什么?
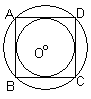 矩形不是正多边形,因为边不一定相等.菱形不是正多边形,因为角不一定相等.
矩形不是正多边形,因为边不一定相等.菱形不是正多边形,因为角不一定相等.
 (三)分析、发现:
(三)分析、发现:
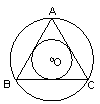
问题:正多边形与圆有什么关系呢?
发现:正三角形与正方形都有内切圆和外接圆,并且为同心圆.
分析:正三角形三个顶点把圆三等分;正方形的四个顶点把圆四等分.要将圆五等分,把等分点顺次连结,可得正五边形.要将圆六等分呢?
2.正方形的边、角各有什么性质?
归纳:等边三角形与正方形的边、角性质的共同点.
教师组织学生进行,并可以提问学生问题.
观察、分析:
1.等边三角形的边、角各有什么性质?
知识小结:通过这节课的学习,使我们知道了对于一组数据,有时只知道它的平均数还不够,还需要知道它的波动大小;而描述一组数据的波动大小的量不止一种,最常用的是方差和标准差.方差与标准差这两个概念既有联系又有区别.
方法小结:求一组数据方差的方法;先求平均数,再利用③求方差,求一组数据标准差的方法:先求这组数据的方差,然后再求方差的算术平方根.
布置作业
教材P173中1,2(1)(2)
板书设计
|
14.3 方差(一) 方差公式③ 引例 例1 标准差公式④ |
4.标准差概念
在有些情况下,需要用到方差的算术平方根
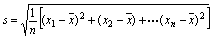 ④
④
并把它叫做这组数据的标准差.它也是一个用来衡量一组数据的波动大小的重要的量.
教师引导学生分析方差与标准差的区别与联系:
计算标准差要比计算方差多开一次平方,但它的度量单位与原数据一致,有时用它比较方便.
课堂练习 教材P165中(1)、(2)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com