26、(1)A　　　 　　　　　　　　

　　　 B　　　　　　　　　　　 -------

和 1,0,-1,-2 ………　　　　　 (2′)

∴P_(和为0)==　　　　　　　(2′)

(2)不公平。　　　　　　　　 (5′)

　　 修改规则：如果和为0，李明得3分，王亮不得分；如果和不为0，则王亮得1分，李明不得分，得分多者获胜。　　　 (7′)

25、设道路宽为xm，(32-x)(20-x)=540　 (3′)

　　　　　　　　　 x₁=50(舍去)，x₂=2　 (5′)

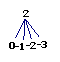
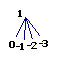　 答：道路宽为2m。　　　　　　　　　　 (6′)

24、略(每个三角形各2分)

23、解：∵△ABC,△DEF为等边三角形。

　　　　 ∴∠B=∠C=∠DEF=60°　　　　 (1′)

　　　　 ∴∠BED+∠FEC=120°　　　 又∠FEC+∠EHC=120°

　　　　 ∴∠BED=∠EHC　　　　　　　 (3′)

　　　　 ∴△DBE∽△ECH　　　　　　　 (5′)

22、(1)原式=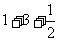　 (2′)　　　　　　 (2) 原式=2-1+2+2　+1　 (2′)

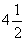　　　　　　 =　　　　 (4′)　　　　　　　　　　 =4+2 　　　　　　(4′)

(3)解：x₁=0，x₂=5　 (4′)　　　　　　 (3)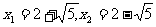　　 (4′)

29、(11分)如图，矩形OABC的两边OA与OC所在的直线为x轴，y轴建立平面直角坐标系，A点的坐标为(3，0)，C点的坐标为(0，4)，将矩形OABC绕O点逆时针旋转，使B点落在y轴的正半轴上，旋转后的矩形为OA₁B₁C₁与BC相交于M.

(1)试说明△B₁CM∽△B₁A₁O，并标出B₁的坐标与线段B₁C的长

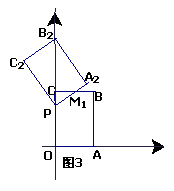
(2)将图1中的矩形OA₁B₁C₁沿y轴向上平移，如图2、图3所示，矩形PA₂B₂C₂是平移过程中的某一位置，BC与矩形的边交于点M₁，点P运动到C点停止，设点P运动的距离为x，CM₁的长为y,求y与x的函数关系式，并写出x的取值范围。

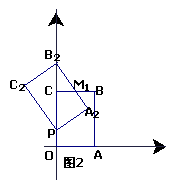(3)在(2)中，试找出这样的X，使矩形PA₂B₂C₂与原矩形OABC重叠部分的面积为。

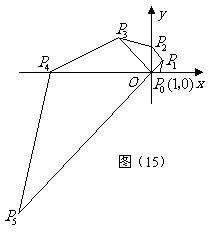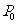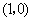28．(10分)如图(15)，在直角坐标系中，已知点的坐标为，将线段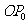按逆时针方向旋转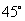，再将其长度伸长为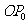的2倍，得到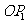线段；又将线段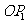按逆时针方向旋转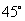，长度伸长为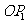的2倍，得到线段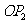；如此下去，得到线段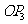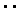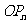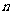，，，(为正整数)

(1)求点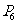的坐标；

(2)求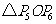的面积；

(3)我们规定：把点()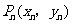

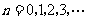的横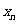坐标、纵坐标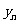都取绝对值后得到的新坐标

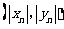称之为点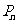的“绝对坐标”．

根据图中点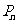的分布规律，请你猜想点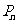的“绝对坐标”，并写出来．

27、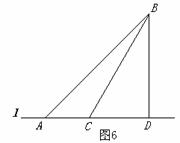(8分)某海滨浴场的海岸线可以看作直线l，有两位救生员在岸边的点A同时接到了海中的点B(该点视为定点)的呼救信号后，立即从不同的路径前往救助。其中1号救生员从点A先跑300米到离点B最近的点D，再跳入海中沿直线游到点B救助；2号救生员先从点A跑到点C，再跳入海中沿直线游到点B救助。如果两位救生员在岸上跑步的速度都是6米/秒，在水中游泳的速度都是2米/秒，且∠BAD=45⁰，∠BCD=60⁰，请问1号救生员与2号救生员谁先到达点B？

25、(6分)如图，在宽为20m， 长为32m的矩形地面上修筑同样宽的道路(图中阴影部分)，余下的部分种上草坪,要使草坪的面积为540m²，求道路的宽。