
常用的数学思想(数学中的四大思想)
1.函数与方程的思想
用变量和函数来思考问题的方法就是函数思想,函数思想是函数概念、图象和性质等知识更高层次的提炼和概括,是在知识和方法反复学习中抽象出的带有观念的指导方法。
深刻理解函数的图象和性质是应用函数思想解题的基础,运用方程思想解题可归纳为三个步骤:①将所面临的问题转化为方程问题;②解这个方程或讨论这个方程,得出相关的结论;③将所得出的结论再返回到原问题中去。
分类讨论的解题步骤一般是:(1)确定讨论的对象以及被讨论对象的全体;(2)合理分类,统一标准,做到既无遗漏又无重复 ;(3)逐步讨论,分级进行;(4)归纳总结作出整个题目的结论。
常用的转化策略有:已知与未知的转化;正向与反向的转化;数与形的转化;一般于特殊的转化;复杂与简单的转化。
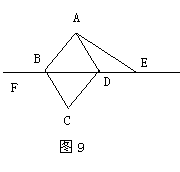
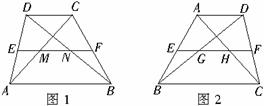
2.如图9,E、F分别是平行四边形ABCD对角线BD所在直线上两点,DE=BF,请你以F为一个端点,和图中已标明字母的某一点连成一条新的线段,猜想并证明它和图中已有的某一条线段相等(只需研究一组线段相等即可)。
(1)连结________;(2)猜想:____________;
(3)证明:
(说明:写出证明过程的重要依据)
北师大2006-2007学年度九年级第一学期第一次模拟测试题
3.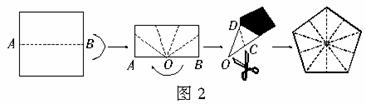 如图2,一张长方形纸片沿
如图2,一张长方形纸片沿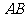 对折,以
对折,以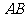 的中点
的中点 为顶点,将平角五等分,并沿五等分线折叠,再从点
为顶点,将平角五等分,并沿五等分线折叠,再从点 处剪开,使展开后的图形为正五边形,则剪开线与
处剪开,使展开后的图形为正五边形,则剪开线与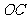 的夹角
的夹角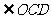 为
为
( )
(A) 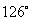 (B)
(B) 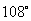 (C)
(C) 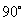 (D)
(D) 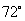
3.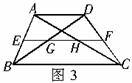 如图3,在梯形
如图3,在梯形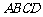 中,
中,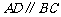 ,中位线
,中位线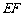 分别与
分别与
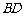 、
、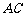 交于点
交于点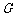 、
、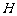 ,若
,若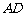 =8,
=8,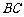 =12,则
=12,则 的值为
( )
的值为
( )
(A) 2 (B) 4
(C) 6 (D) 8
2.如图2,梯形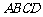 中,
中,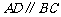 ,
,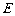 、
、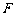
分别是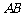 、
、 的中点,
的中点,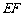 交
交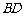 于
于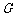 ,交
,交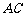
于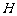 ,若
,若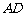 =2,
=2,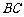 =5,则
=5,则 =______
;
=______
;
1. 如图1,在梯形
如图1,在梯形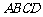 中,
中,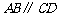 ,中位线
,中位线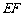 与对角线
与对角线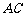 、
、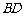 交于
交于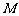 、
、 两点,若
两点,若 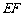 =18
=18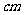 ,
, =8cm ,则
=8cm ,则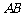 的长等于
( )
的长等于
( )
(A) 10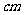 (B) 13
(B) 13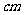
(C) 20 (D) 26
(D) 26
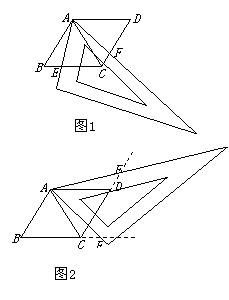
25.用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合,使三角尺的60°角的顶点与点A重合,两边分别与AB,AC重合.将三角尺绕点A按逆时针方向旋转.
(1)(5分)当三角尺的两边分别与菱形的两边BC,CD相交于点E,F时,(如图1),通过观察或测量BE,CF的长度,你能得出什么结论?并证明你的结论;
(2)(5分)当三角尺的两边分别与菱形的两边BC,CD的延长线相交于点E,F时(如图2),你在(1)中得到的结论还成立吗?简要说明理由.
家庭作业:(改错时做)
24.(6分)宏达汽车租赁公司有出租车120辆,每辆汽车的日租金为160元,出租车业务天天供不应求,为适应市场需求,公司准备适当提高日租金,经市场调查发现,一辆汽车的日租金每增加10元,每天出租的汽车相应的减少6辆,该公司的日租金提高多少元时,可使租金总收入达到19440元?
23.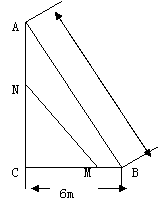 (6分)如图,在直角ΔABC中,∠C=90o ,BC= 6
(6分)如图,在直角ΔABC中,∠C=90o ,BC= 6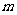 , AB=10
, AB=10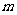 . 点M从B点以1
. 点M从B点以1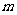 /s的速度向点C匀速移动,同时点N从C点以2
/s的速度向点C匀速移动,同时点N从C点以2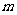 /s的速度向点A匀速移动,问几秒钟后,ΔMNC的面积是ΔABC面积的
/s的速度向点A匀速移动,问几秒钟后,ΔMNC的面积是ΔABC面积的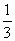 ?
?

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com