
例6 已知关于x的一次函数y=mx+3n和反比例函数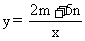 的图象都经过点(1,-2).求:
的图象都经过点(1,-2).求:
(1)一次函数和反比例函数的解析式;
(2)两个函数图象的另一个交点的坐标.
解析:(1)∵两函数图象都过点(1,-2),

∴一次函数的解析式为y=4x-6,

(2)根据题意,列出方程组
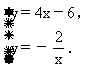
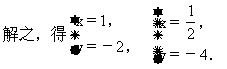
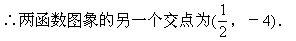
评注:
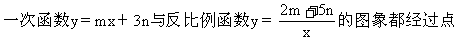
(1,-2),则该点坐标满足两解析式;要求两图象交点,则应由两图象的解析式组成方程组求解.


(1)k满足什么条件时,这两个函数在同一坐标系xOy中的图象有两个公共点?
(2)设(1)中的两个公共点为A,B,试判断∠AOB是锐角还是钝角?

消去y,得x2-6x+k=0.
∵Δ=36-4k>0,∴k<9.
当k<9且k≠0时,方程x2-6x+k=0有两个不相等的非零实数解.
∴k<9且k≠0时,两函数图象有两个公共点.
(2)∵y=-x+6的图象过第一,二,四象限,
∴0<k<9时,双曲线两支分别在第一、三象限.由此知两公共点
A,B在第一象限,此时∠AOB是锐角.
k<0时,双曲线两支分别在第二,四象限,两公共点A,B分别在第二、四象限,此时∠AOB是钝角.


(1)求m的值;
(2)若直线l分别与x轴、y轴相交于E,F两点,并且Rt△OEF(O是坐标原点)的外心为点A,试确定直线l的解析式;
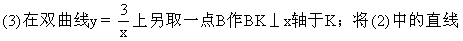
l绕点A旋转后所得的直线记为l′,若l′与y轴的正半轴相交于点C,

若存在,请求出点P的坐标?若不存在,请说明理由.
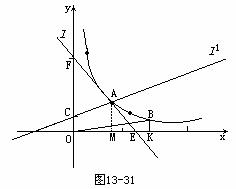
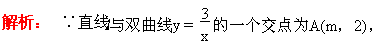

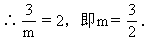
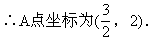
(2)作AM⊥x轴于M.
∵A点是Rt△OEF的外心,
∴EA=FA.
由AM∥y轴有OM=ME.
∴OF=2OM.
∵MA=2,∴OF=4.
∴F点的坐标为(0,4).
设l:y=kx+b,则有
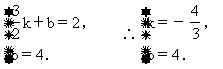
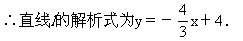
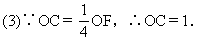
∴C点坐标为(0,1).
设B点坐标为(x1,y1,),则
x1y1=3.
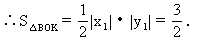
设P点坐标为(0,y),满足S△PCA=S△BOK.
①当点P在C点上方时,y>1,有
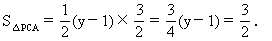
∴y=3.
②当点P在C点下方时,y<1,有
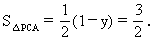
∴y=-2.
综上知,在y轴存在点P(0,3)与(0,-2),使得S△PAC=S△BOK.
评注:直线与双曲线的综合题的重要组成部分是两种图象的交点,这是惟一能沟通它们的要素,应用交点时应注意:
(1)交点既在直线上也在双曲线上,交点坐标既满足直线的解析式也满足双曲线的解析式.
(2)要求交点坐标时,应将两种图象对应的解析式组成方程组,通过解方程组求出交点坐标.
(3)判断两种图象有无交点时,可用判别式确定,也可以画出草图直观地确定.


上的两点,直线CD分别交x轴,y轴于A,B两点,设C,D的坐标分别是(x1,y1),(x2,y2),连结OC,OD.
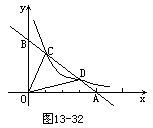
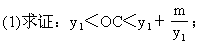
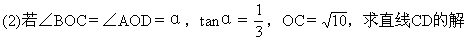
析式.
证明:(1)如图13-33过点C作CG⊥x轴,垂足为G,则CG=y1,OG=x1.
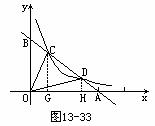

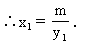
∵在Rt△OCG中,CG<OC<CG+OG,
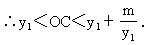
解(2):在Rt△GCO中,∠GCO=∠BOC=α,
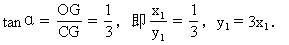
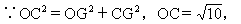
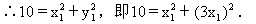
解之,得x1=±1.
∵负值不合题意,∴x1=1,y1=3.
∴点C的坐标为(1,3),
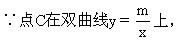
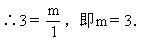

过点D作DH⊥x轴,垂足为H.则DH=y2,OH=x2.
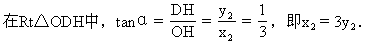
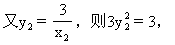
解之得y2=±1.
∵负值不合题意,∴y2=1,x2=3.
∴点D的坐标为(3,1).
设直线CD的解析式为y=kx+b.
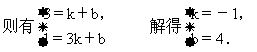
∴直线CD的解析式为y=-x+4.
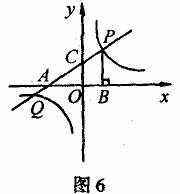
例6.如图6,直线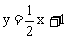 分别交x轴、y轴于点A,C,点P是直线AC与双曲线
分别交x轴、y轴于点A,C,点P是直线AC与双曲线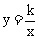 在第一象限内的交点,
在第一象限内的交点,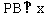 轴,垂足为点B,
轴,垂足为点B,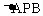 的面积为4。
的面积为4。
(1)求点P的坐标;(2)略。
析解:在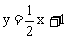 中,令
中,令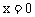 ,则
,则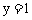 ;令
;令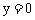 ,则
,则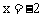 。
。
所以点A的坐标为(-2,0),点C的坐标为(0,1)。
因为点P的直线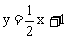 上,
上,
不妨设点P的坐标为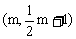
所以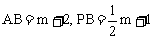 。
。
又因为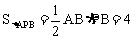
所以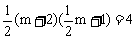
整理得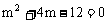
即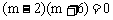
解得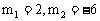
因为点P在第一象限,所以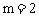 。
。
故点P的坐标为(2,2)。
评注:本题的解答过程蕴含着设元思想、方程思想和转换思想。
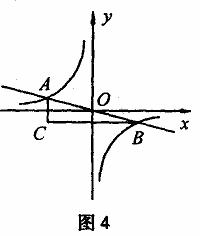
例4.如图4,反比例函数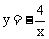 的图象与直线
的图象与直线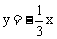 的交点为A,B,过点A作y轴的平行线与过点B作x轴的平行线相交于点C,则
的交点为A,B,过点A作y轴的平行线与过点B作x轴的平行线相交于点C,则 的面积为( )
的面积为( )
A. 8 B. 6 C. 4 D. 2
解析:把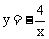 代入
代入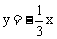 ,得
,得
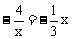
整理得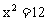
解得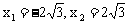
把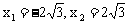 分别代入
分别代入
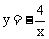 ,
,
得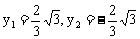
所以点A的坐标为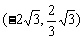
点B的坐标为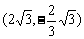
由题意知,点C的横坐标与点A的横坐标相同,点C的纵坐标与点B的纵坐标相同,所以点C的坐标为(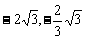 )。
)。
因为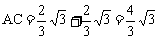 ,
,
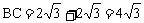
所以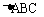 的面积为
的面积为
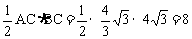
故应选A。
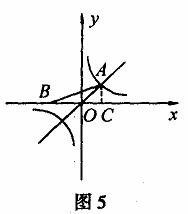
例5.如图5,已知点A是一次函数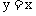 的图象与反比例函数
的图象与反比例函数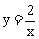 的图象在第一象限内的交点,点B在x轴的负半轴上,且OA=OB,那么
的图象在第一象限内的交点,点B在x轴的负半轴上,且OA=OB,那么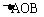 的面积为( )
的面积为( )
A. 2 B.
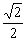 C.
C.
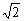 D.
D.
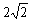
析解:把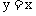 代入
代入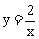 ,得
,得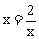 ,
,
整理得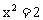 ,解得
,解得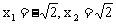
得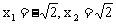 分别代入
分别代入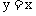
得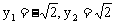
又点A在第一象限内,所以点A的坐标为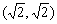
在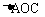 中
中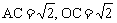
由勾股定理,得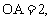 所以OB=2。
所以OB=2。
所以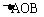 的面积为
的面积为
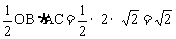 ,
,
故应选(C)
评注:例4和例5中都利用解方程来求出两函数图象的交点坐标,这是求两函数图象交点坐标的常用方法,蕴含着转化思想。
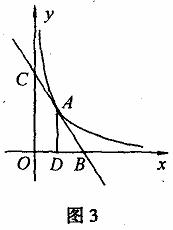
例3.如图3,直线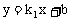 与双曲线
与双曲线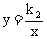 只有一个交点A(1,2),且与x轴,y轴分别交于B,C两点,AD垂直平分OB,垂足为D,求直线与双曲线的解析式。
只有一个交点A(1,2),且与x轴,y轴分别交于B,C两点,AD垂直平分OB,垂足为D,求直线与双曲线的解析式。
解析:因为双曲线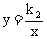 过点A(1,2),
过点A(1,2),
所以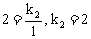
得双曲线的解析式为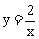 。
。
因为AD垂直平分OB,A点的坐标为(1,2)。所以B点的坐标为(2,0)。
因为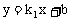 过点A(1,2)和B(2,0),
过点A(1,2)和B(2,0),
所以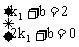
解得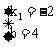
所以直线的解析式为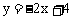
评注:解决本题的关键是确定点B的坐标,由AD垂直OB知,点D和点A的横坐标应相同,所以点D的坐标为(1,0),又AD平分OB知,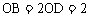 ,所以点B坐标为(2,0),进而求出一次函数解析式。
,所以点B坐标为(2,0),进而求出一次函数解析式。
例1. 已知函数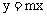 与
与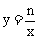 在同一直角坐标系中的图象大致如图1,则下列结论正确的是( )
在同一直角坐标系中的图象大致如图1,则下列结论正确的是( )
A. 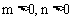 B.
B.
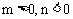
C. 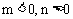 D.
D.
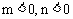
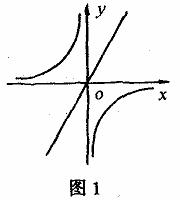
分析:由图知,一次函数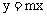 中,y随x的增大而增大,所以
中,y随x的增大而增大,所以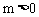 ;反比例函数
;反比例函数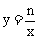 在第二、四象限,所以
在第二、四象限,所以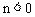 。观察各选项知,应选B。
。观察各选项知,应选B。
评注:本题要由所给图象结合一次函数和反比例函数的性质,方能作出正确选择。
例2.在同一直角坐标系中,函数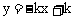 与
与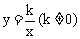 的图象大致是( )
的图象大致是( )
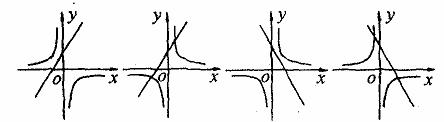
A. B. C. D.
图2
分析:本题可采用排除法。由选项A、B的一次函数图象知,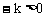 即
即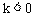 ,则一次函数
,则一次函数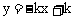 图象与y轴交点应在y轴负半轴,而选项A、B都不符合要求,故都排除;由选项D的一次图象知,
图象与y轴交点应在y轴负半轴,而选项A、B都不符合要求,故都排除;由选项D的一次图象知,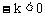 即
即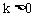 ,则反比例函数
,则反比例函数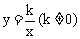 图象应在第一、三象限,而选项D不符合要求,故也排除;所以本题应选C。
图象应在第一、三象限,而选项D不符合要求,故也排除;所以本题应选C。
评注:本题把一次函数和反比例函数的图象在同一坐标系中给出,有较强的综合性,解决这类问题常用排除法。
29.
2007-2008学年度第一学期期末测试七年级数学练习卷(二)
27
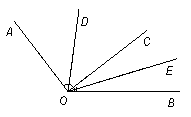
28.
26.
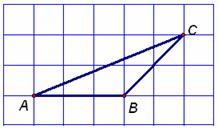 (3) 点C到直线AB的距离为 .
(3) 点C到直线AB的距离为 .
25.
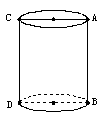
16. . 17. . 18. .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com