40、(江西)如图，正三角形ABC的边长为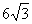厘米，⊙O的半径为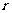厘米，当圆心O从点A出发，沿着线路AB→BC→CA运动，回到点A时，⊙O随着点O的运动而移动。

(1)若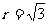厘米，求⊙O首次与BC边相切时，AO的长。

(2)在⊙O移动过程中，从切点的个数来考虑，相切有几种不同的情况？写出不同的情况下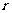，的取值范围及相应的切点的个数。

(3)设⊙O在整个移动过程中，在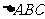的内部，⊙O未经过的部分的面积为S，在S＞0时，求S关于r的函数解析式，并写出自变量r的取值范围。

39、(黑龙江)已知等边△ABC和点P，设点P 到△ABC三边AB、AC、BC 的距离分别为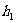、、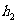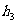，△ABC的高为。

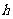“若点P在一边BC上，如图(一)，此时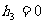，可得结论：。”

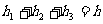请直接应用上述信息解决下列问题：

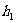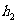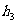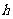当点P在△ABC内，如图(二)，点P在△ABC外，如图(三)这两种情况时，上述的结论是否成立？若成立，请给予证明；若不成立，、、与之间又有怎样的关系，请写出你的猜想，不需证明。

38、(北京宣武)已知：如图，在 Rt△ABC中，∠C＝90⁰，沿过B点的一条直线BE折叠这个三角形，使C点与AB边上的一点D重合。当∠A满足什么条件时，点D恰为AB的中点？写出一个你认为适当的条件，并利用此条件证明D为AB中点。　　　　　　　　　　　　　　　　　　

37、(江西)如图，AB＝AE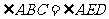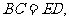，，点F是CD的中点。

(1)求证：AF⊥CD；

(2)在你连结BE后，还能得出什么新的结论？请写出三个(不要求证明)。

36、(安徽)某学习小组在探索“各内角都相等的圆内接多形是否为正多边形”时，进行如下讨论：

甲同学：这种多边形不一定是正多边形，如圆内接矩形；

乙同学：我发现边数是6时，它也不一定是正多边形，如图(1)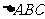，是正三角形，AD＝BE＝CF，可以证明六边形ADBECF的各内角相等，但它未必是正六边形；

丙同学：我能证明，边数是5时，它是正多边形，我想边数是7时，它可能也是正多边形。

… …

(1)请你说明乙同学构造的六边形各内角相等。

(2)请你证明，各内角相等的圆内接七边形ABCDEFG是正七边形，如图(2)，(不必写已知、求证)。

(3)根据以上的探索过程，提出你的猜想(不必证明)。

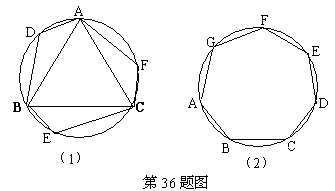
35、(山东济南)如图，⊙为O表示一圆形纸版，根据要求， 需要通过多次剪裁，把它前剪成若干个扇形面。操作过程如下：第一次剪裁，将圆形纸版等分为4个扇形；第2次裁，将上次得到的扇形面中的一个再等分成4个扇形；以后按第2次剪裁的作法进行下去。

(1)请你在⊙O中，用尺规作出第2次剪裁后得到的7个扇形(保留痕迹，不写作法)；

(2)请你通过操作和猜想，将第3次、第4次和第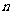次裁剪后所得扇形的总个数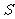填入下表：

等分圆及扇形面的次数(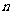)	1	2	3	4	…
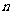所得扇形的总个数(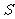)	4	7			…

(3)请你推断，能不能按上述操作过程，将原来的圆形纸板剪成33个扇形？为什么？

34、(湖北荆州市) 有一块方角形钢板如图所示，请你用一条直线将其分为面积相等的两部分(不写作法，保留作图痕迹，在图中直接画出)。

33、(湖北黄冈市) 在一服装厂里有大量形状为等腰直角三角形的边角布料(如图24)，其直角边长为4。今要从这种三角形中剪出一种扇形，做成不同形状的玩具，使扇形的边缘半径恰好在三角形的边上，且扇形的弧与三角形的其他边相切。请设计出所有可能符合题意的方案示意图，并求出扇形的半径(只要求画出图形，并直接写出扇形半径)。

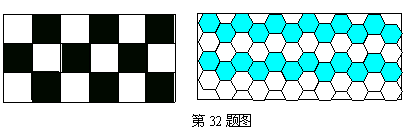
32、(浙江)如图，人们常常用正方形或正六边形的地板砖铺地面，这样能够铺得平整、无空隙。

(1)请问能不能全用正五边形的地板砖铺地面，为什么？

(2)请问能否另外想出一个全用一种形状的(不一定是正方形)地板砖铺地面的方案，使铺成的地面美观、平整、无空隙，画出这个方案的草图；

(3)请你设计一个用两种形状的地板砖铺地面的方案，使铺成的地面美观、平整、无空隙，画出这个方案的草图即可。

31、(绍兴)如图、某斜拉桥的一组钢索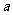、、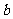、、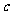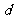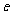共五条，它们相互平行，钢索与桥面的固定点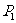、、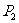、、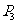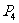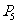中，每相邻两点等距离。

(1)问至少需知道几条钢索的长，才能计算出其余钢索的长？

(2)请你对(1)中需知道的这几条钢索长给 出具体的数值，并由此计算出其余钢索的长。