
6. 如果等腰梯形两底之差等于一腰长, 那么这个等腰梯形的一个锐角是 ____________
5. 三角形三条边长分别为8, 15, 17, 那么最短边上的高是_______________
4. 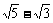 的倒数是 ________________;
的倒数是 ________________; 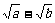 的相反数是 _______________
的相反数是 _______________
3. 正比例函数y = ax
(a ¹0 ) 与反比例函数y =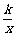 (k¹0 ) 的图象有一个交点坐标是
(2, 4), 则它的另一个交点坐标是 _____________
(k¹0 ) 的图象有一个交点坐标是
(2, 4), 则它的另一个交点坐标是 _____________
1. 当x ___________ 时, 式子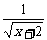 有意义
有意义
|
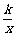 (k¹0 )的图象经过点P如图所示,
根据图象可知, 反比例函数的解析式为 _____________________
(k¹0 )的图象经过点P如图所示,
根据图象可知, 反比例函数的解析式为 _____________________25. (10分) (2008恩施自治州)如图8,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=5,DE=1,BD=8,设CD=x.
(1)用含x的代数式表示AC+CE的长;
(2)请问点C满足什么条件时,AC+CE的值最小?
(3)根据(2)中的规律和结论,请构图求出代数式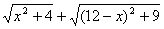 的最小值.
的最小值.

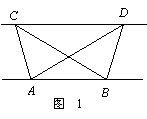
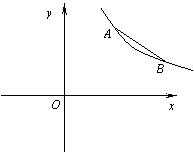
24. (10分) (08东营、莱芜市)(1)探究新知:如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由.
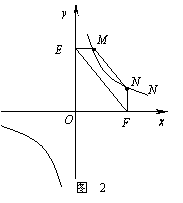
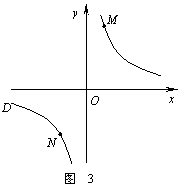
(2)结论应用:① 如图2,点M,N在反比例函数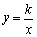 (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.试证明:MN∥EF.②
若①中的其他条件不变,只改变点M,N的位置如图3所示,请判断 MN与EF是否平行.
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.试证明:MN∥EF.②
若①中的其他条件不变,只改变点M,N的位置如图3所示,请判断 MN与EF是否平行.
23. (10分)(08威海)如图,点A(m,m+1),B(m+3,m-1)都在反比例函数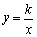 的图象上.
的图象上.
(1)求m,k的值;
(2)如果M为x轴上一点,N为y轴上一点, 以点A,B,M,N为顶点的四边形是平行四边形,试求直线MN的函数表达式.
22. (10分)
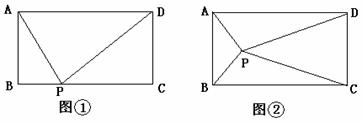
(08莆田)已知矩形ABCD和点P,当点P在BC上任一位置(如图(1)所示)时,易证得结论: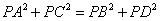 ,请你探究:当点P分别在图(2)、图(3)中的位置时,
,请你探究:当点P分别在图(2)、图(3)中的位置时,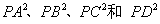 又有怎样的数量关系?请你写出对上述两种情况的探究结论,并利用图(2)证明你的结论。
又有怎样的数量关系?请你写出对上述两种情况的探究结论,并利用图(2)证明你的结论。
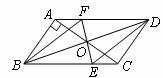
21. (10分)(08兰州)如图,平行四边形 中,
中,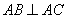 ,
, ,
,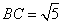 .对角线
.对角线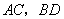 相交于点
相交于点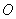 ,将直线
,将直线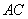 绕点
绕点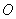 顺时针旋转,分别交
顺时针旋转,分别交 于点
于点 .
.
(1)证明:当旋转角为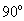 时,四边形
时,四边形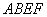 是平行四边形;
是平行四边形;
(2)试说明在旋转过程中,线段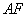 与
与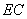 总保持相等;
总保持相等;
(3)在旋转过程中,四边形 可能是菱形吗?如果不能,请说明理由;如果能,说明理由并求出此时
可能是菱形吗?如果不能,请说明理由;如果能,说明理由并求出此时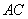 绕点
绕点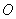 顺时针旋转的度数.
顺时针旋转的度数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com