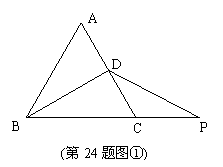
24．(本题满分12分)如图，△ABC是等边三角形，BD是

中线，P是直线BC上一点．

(1) 若CP=CD，求证：△DBP是等腰三角形；

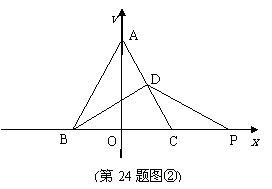(2) 在图①中建立以△ABC的边BC的中点为原点，BC所在直线为x轴，BC边上的高所在直线为y轴的平面直角坐标系，如图②，已知等边△ABC的边长为2，AO=，在x轴上是否存在除点P以外的点Q，使△BDQ是等腰三角形？如果存在，请求出Q点的坐标；如果不存在，请说明理由．

潮阳实验学校2008-2009学年度第一学期期中考试

八年级数学

23．(本题满分12分)某汽车租赁公司要购买轿车和面包车共10辆，其中轿车至少要购3辆．轿车每辆7万元，面包车每辆4万元．公司投入购车的资金不超过58万元，设购买轿车为x辆，所需资金为所需资金为y万元．

(1)写出y与x的函数关系式；

(2)求出自变量x的取值范围；

(3)若公司投入资金为52万元，问轿车和面包车各购多少辆？

22．(本题满分12分)如图，△ABC中，AB=AC，∠BAC=90°，直线l经过点A，过点B作BE⊥l于E，过点C作CF⊥l于F．

(1)求证：EF=BE+CF；

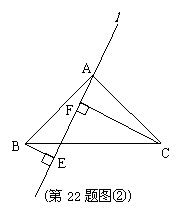
(2)将直线绕点A旋转到图②的位置，其它条件不变，

EF=BE+CF仍然成立吗？如果不成立，线段EF、BE、CF

又有怎样的关系？请说明理由。

21．(本题满分9分)如图，在△AFD和△BEC中，点A、E、F、C在同一直线上，有下面四个论断：①AD=CB，②AE=CF，③∠B=∠D，④AD∥BC．请用其中三个作为已知条件，余下一个作为求证结论，编一道数学问题，并写出解答过程：

已知条件：　　　 ，　　　　，　　　　 ；

求证结论：　　　 ．

证明：

20．(本题满分9分)已知△PQR在直角坐标系中的位置如图所示：

(1) 求出△PQR的面积；

(2) 画出△P′Q′R′，使△P′Q′R′与△PQR

关于y轴对称，写出点P′、Q′、R′的坐标；

(3)连接PP′，QQ′，判断四边形QQ′P′P的

形状，求出四边形QQ′P′P的面积．

19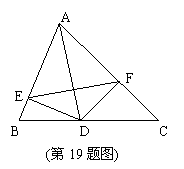．(本题满分9分)如图，AD是△ABC的角平分线，DE，DF分别是△ABD和△ACD的高．AD和EF有什么关系？请说明理由．

18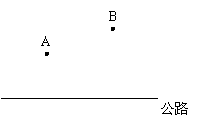．(本题满分7分)需要在高速公路旁边修建一个飞机场，使飞机场到A，B两个城市的距离之和最小，请作出机场的位置．

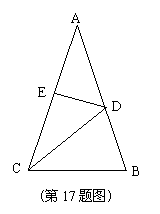
17．(本题满分7分)如图，在△ABC中，AB=AC，∠A=30º，

DE垂直平分AC于E，连结CD，求∠DCB的度数．

16．(本题满分7分)求下列方程中x的值：

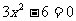
15．(本题满分7分)如图，在网格中有两个全等的图形(阴影部分)，用这两个图形拼成轴对称图形，试分别在图(1)、(2)中画出两种不同的拼法．