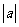3．a是一个无理数，且满足3＜＜4，则a可能是( 　　 )

A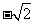．　　　 B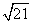．　　　　 C．π　　　 D．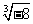

2．下列说法中正确的是(　 　 )

A．36的平方根是6　　　　 B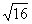．的平方根是±2

C．8的立方根是－2　　　　 D．4的算术平方根是－2

1．下列银行标志中是轴对称图形的个数有(　 　　 )

A．2个　　　 　B．3个　　　 　 C．4个　　 　 D．5个

24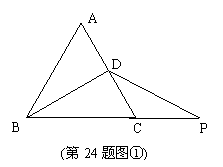．(本题满分12分)

证明：∵△ABC是等边三角形

∴∠ABC=∠ACB=60°

∵BD是中线

∴∠DBC=30°

∵CP=CD 　……………………………2分

∴∠CPD=∠CDP

又∵∠ACB=60°

∴∠CPD=30° ……………………………4分

∴∠CPD=∠DBC

∴DB=DP ……………………………6分

即△DBP是等腰三角形．

(2)

解：在x轴上存在除点P以外的点Q，使△BDQ是等腰三角形

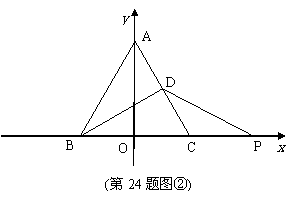①若点P在x轴负半轴上，且BP=BD

∵BD=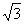

∴BP=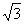

∴OP=

∴点P₁(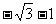，0)……………8分

②若点P在x轴上，且BP=PD

∵∠PBD=∠PDB=30°

∴∠DPC=60°

又∠PCD=60°

∴PC=DC=1

而OC=1

∴OP=0

∴点P₂(0，0)…………………………10分

③若点P在x轴正半轴上，且BP=BD

∴BP=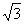

而OB=1

∴OP=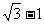

∴点P₃(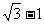，0) …………………………12分

23．(本题满分12分)

解：(1) 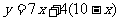即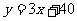 ……………………………4分

(2)∵

∴

∴

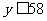
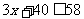
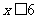
　　　 且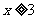

∴自变量x的取值范围是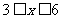且x为正整数．……………………………8分

(3)∵

∴

∴

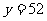
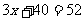
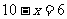∴ …………………………12分

答：

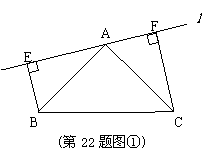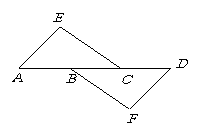
22．( (1)求证：EF=BE+CF；

证明：∵BE⊥l，CF⊥l

∴∠AEB=∠CFA=90°

∴∠EAB+∠EBA=90°

又∵∠BAC=90°

∴∠EAB+∠CAF=90°

∴∠EBA=∠CAF …………………………2分

在△ADF和△CBE中

　　　 ∠AEB=∠CFA

∠EBA=∠CAF

AB=AC

∴△ADF≌△CBE ……………………………5分

∴AE=CF，BE=AF

∴AE+AF=BE+CF

即EF=BE+CF…………………………… 6分

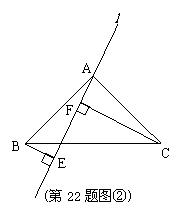(2)

解： EF=BE+CF不成立。EF=BE+CF，理由如下

∵BE⊥l，CF⊥l

∴∠AEB=∠CFA=90°

∴∠EAB+∠EBA=90°

又∵∠BAC=90°

∴∠EAB+∠CAF=90°

∴∠EBA=∠CAF ……………………………8分

在△ADF和△CBE中

∠AEB=∠CFA

∠EBA=∠CAF

AB=AC

∴△ADF≌△CBE …………………………11分

∴AE=CF，BE=AF

∴AE+AF=BE+CF

即EF=BE+CF…………………………12分

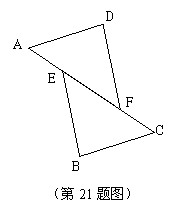
21．(本题满分9分)

已知条件：　AD=BC　 ，　AE=CF　，　AD∥BC　　 ；

求证结论：　∠B=∠D ．……………………………4分

证明：∵AE=CF

∴AE+EF=CF+EF

∴AF=CE

∵AD∥BC

∴∠A=∠C ……………………………6分

在△ADF和△CBE中

AD=BC

∠A=∠C

AF=CE

∴△ADF≌△CBE　

∴∠B=∠D ……………………………9分

20．(本题满分9分)

解：(1) S△PQR=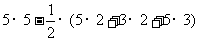

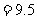　……………………………2分

(2) △P′Q′R′就是所要画的三角形

各点坐标分别为P′(4,-1)、Q′(1,4)、

R′(-1,1)；……………………………7分

(3)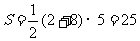．……………………………9分

19．(本题满分9分)解：AD垂直平分EF，理由如下　 ……………………………2分

∵AD是△ABC的角平分线，

且DE，DF分别是△ABD和△ACD的高

∴DE=DF，∠DEA=∠DFA=90 º

　 　在Rt△AED和△AFD中

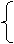　　　 AD=AD

DE=DF

∴Rt△AED≌△AFD ………………7分

∴AE=AF

又DE=DF

∴AD垂直平分EF……………………………9分