
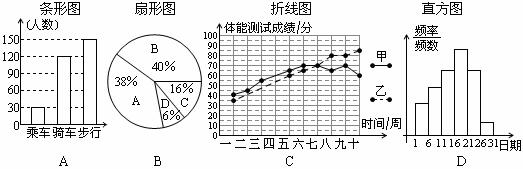
3.在数据统计中,条形图、扇形图、折线图和直方图各有特点,下列各图中,能够很好地显示数据的变化趋势的统计图是( )
2.在△ABC和△A1B1C1中,由AB=A1B1,BC=B1C1,AC=A1C1,得出△ABC≌△A1B1C1的根据是( )
A.SSS B.SAS C.AAS D.HL
1.下列点的坐标中,在直线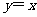 上的点的坐标是( )
上的点的坐标是( )
A.(1,2007) B.(2007,1)
C.(2007,2007) D.(-2007,2007)
25、(本题12分)
(1)∵OA=OB=OC,∠AOC=∠BOC=90°
∴∠OAC=∠OCA=∠OBC=∠OCB=45°
∴∠ACB=90° ……1分
又△ABC的面积为9,
∴OA=OC=OB=3 ……2分
∴A(-3,0),B(3,0),C(0,-3) ……4分
(2)当t=3秒时,即CP=OC时,DP与DB垂直且相等. ……5分
理由如下:
连结OD,作DM⊥x轴于点M,作DN⊥y轴于点N
∵D(-m,-m)
∴DM=DN=OM=ON=m
∴∠DOM=∠DON=45°
而∠ACO=45°
∴DC=DO
∴∠PCD=∠BOD=135°
又CP=OC=OB
∴△PCD≌△BOD (SAS) ……7分
∴DP=DB,∠PDC=∠BDO
∴∠BDP=∠ODC=90°
即DP⊥DB. ……8分
(3)解:①正确.
在QA上截取QS=QP,连结PS. ……9分
∵∠PQA=60°
∴△QSP是等边三角形
∴PS=PQ,∠SPQ=60°
∵PO是AB的垂直平分线
∴PA=PB
而PA=AB
∴PA=PB=AB
∴∠APB=60°
∴∠APS=∠BPQ
∴△APS≌△BPQ ……11分
∴∠PAS=∠PBQ
∴∠APQ+∠PBQ=∠APQ+∠PAS=180° ……12分
注:不同于此标答的解法请参照此标答给分.
24、(本题10分)
(1)①垂直(或BD⊥CE),相等(或BD=CE);(每空1分) ……2分
②①中的结论是否仍然成立,理由如下
∵∠BAC=∠DAE=90º
∴∠BAD=∠CAE
又AB=AC,AD=AE
∴△ABD≌△ACE (SAS) ……4分
∴BD=CE,∠B=∠ACE ……5分
而∠B+∠ACB=90º
∴∠ACE+∠ACB=∠BCE=90º
即BD⊥CE ……6分
(2)画图正确(图略) ……8分
当△ABC满足∠ACB=45°时,BC⊥CE . ……10分
23、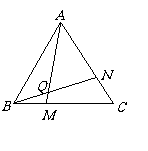 (本题10分)
(本题10分)
(1)证明:∵△ABC是等边三角形
∴∠ABM=∠C=60°,AB=BC ……2分
又∠ABQ+∠BAQ=∠BQM=60°
∠ABQ+∠CBN=∠ABM=60°
∴∠BAQ=∠CBN ……3分
∴△ABM≌△BCN (ASA) ……4分
∴BM=CN (全等三角形对应边相等) ……5分
(2)解:仍能得到BM=CN,如图所示.证明如下: ……6分
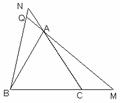 ∵△ABC是等边三角形
∵△ABC是等边三角形
∴∠ABC=∠ACB=60°,AB=BC ……7分
又∠M+∠MAC=∠ACB=60°
∠N+∠NAQ=∠BQM=60°
而∠MAC=∠NAQ (对顶角相等)
∴∠M=∠N ……8分
∴△ABM≌△BCN (AAS) ……9分
∴BM=CN (全等三角形对应边相等) ……10分
22、(本题8分)
证明:∵PE⊥OA,PF⊥OB
∴∠OEP=∠OFP
又∠AOC=∠BOC
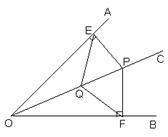 ∴∠OPE=∠OPF
……1分
∴∠OPE=∠OPF
……1分
即OP平分∠EPF
∴OE=OF ……4分
在△OEQ和△OFQ中
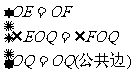
∴△OEQ≌△OFQ (SAS) ……7分
∴QE=QF ……8分
21、(本题7分)解:图中有3对全等三角形,分别是:
△ABF≌ △DEC ;△FBC≌ △CED;△ABC≌ △DEF. (对1个得1分)
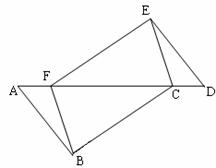 ……3分
……3分
对△ABF≌ △DEC进行证明如下:
∵AB∥DE
∴∠A=∠D ……4分
在△ABF和△DEC中
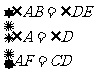
∴△ABF≌ △DEC (ASA) ……7分
20、(本题7分)
答:彬彬的作法正确. ……1分
证明:作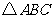 的角平分线
的角平分线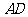
则∠BAD=∠CAD ……2分
在△BAD和△CAD中
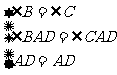
∴△BAD≌△CAD(AAS) ……5分
∴AB=AC(全等三角形对应边相等) ……7分
19、(本题6分)上午8时,一条船从海岛A出发,以15海里/时的速度向正北航行,10时到达海岛B处,从A,B望灯塔C,测得∠NAC=43°,∠NBC=86°.问海岛B与灯塔C相距多远?
解:∵∠NAC=43°,∠NBC=86°
∴∠ACB=43° ……2分
∴∠NAC=∠ACB
∴BC=BA=15×2=30 ……5分
答:海岛B与灯塔C相距30海里 ……6分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com