
4、 梯形ABCD中,AD∥BC,AB=CD,对角线AC=BC+AD,则∠ACB的度数是(
)
梯形ABCD中,AD∥BC,AB=CD,对角线AC=BC+AD,则∠ACB的度数是(
)
A.30° B.45° C.90° D.60°
3、下列命题中假命题是( )
A.对角线相等的菱形是正方形;B.一组邻边相等的平行四边形是正方形;
C.对角线互相平分且相等的四边形是矩形; D.对角线互相垂直平分的四边形是菱形
2、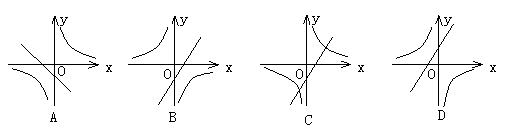 已知函数y=k (x-1)和
已知函数y=k (x-1)和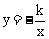 (k≠0),它们在同一坐标系内的图象大致是( )
(k≠0),它们在同一坐标系内的图象大致是( )
1、如果函数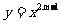 为反比例函数,则
为反比例函数,则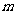 的值是( )
的值是( )
A.-1;
B.0;
C.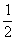 ;
D.1。
;
D.1。
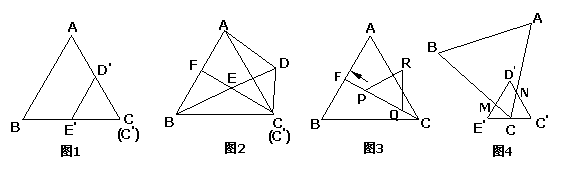
28.(10分)图1是边长分别为4和3的两个等边三角形纸片ABC和C′D′E′叠放在一起(C与C′重合)。
(1)操作:固定△ABC,将△C′D′E′绕点C顺时针旋转30°得到△CDE,连结AD、BE,CE的延长线交AB于F(图2);
探究:在图2中,线段BE与AD之间有怎样的大小关系?试证明你的结论。
(2)操作:将图2中的△CDE,在线段CF上沿着CF方向以每秒1个单位的速度平移,平移后的△CDE设为△PQR(图3);
请问:经过多少时间,△PQR与△ABC重叠部分的面积恰好等于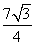 ?
?
(3)操作:图1中△C′D′E′固定,将△ABC移动,使顶点C落在C′E′的中点,边BC交D′E′于点M,边AC交D′C′于点N,设∠AC C′=α(30°<α<90,图4);
探究:在图4中,线段C N·E
N·E M的值是否随α的变化而变化?如果没有变化,请你求出C
M的值是否随α的变化而变化?如果没有变化,请你求出C N·E
N·E M的值,如果有变化,请你说明理由。
M的值,如果有变化,请你说明理由。
2007年重庆一中初二下学期期末测试
27.(10分) 某商场于第一年初投入50万元进行商品经营,以后每年年终将当年获得的利润与当年年初投入的资金相加所得的总资金,作为下一年年初投入的资金继续经营。
(1)如果第一年的年获利率为P,第二年的年获利率恰好与第一年相同,那么第二年年终的总资金是多少万元?(用含P的代数式表示;注:年获利率 = 年利润/年初投入的资金×100%)
(2)如果第二年的年获利率比第一年的年获利率多10个百分点(即第二年的年获利率是第一年的年获利率与10%的和),第二年年终的总资金为66万,求第一年的年获利率。
26.(8分)下面是芩芩用换元法解方程2(x+1)2+3(x+1)(x―2)―2(x―2)2=0的解答过程,请你判断是否正确。若有错误,请按上述思路求出正确答案。
解:
设 +1=m,
+1=m,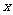 -2=n, 则原方程可化为: 2m2+3mn-2n2=0,
-2=n, 则原方程可化为: 2m2+3mn-2n2=0,
即a=2,b=3n,c=-2n2。
∴m=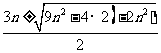 =
= 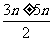
即 m1=4n,m2=-n。
所以有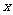 +1=4(
+1=4(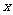 -2)或
-2)或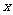 +1=-(
+1=-(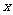 -2),
-2),
∴x1=3,x2=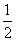 。
。
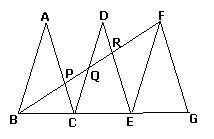
25.(8分)如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=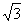 ,BC=1。连结BF,分别交AC、DC、DE于点P、Q、R。
,BC=1。连结BF,分别交AC、DC、DE于点P、Q、R。
(1)求证:△BFG∽△FEG;
(2)求出BF的长。
24.(8分)已知关于x的方程x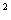 +mx+n=0的根为2和-2,求x
+mx+n=0的根为2和-2,求x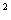 +nx+m=0的两根。
+nx+m=0的两根。
23.(8分)我校初2008级的小明和小兵一直在校田径队接受某一项目的专项训练,在上月
举行的市中学生田径运动会前夕,教练对二人进行了测试,8次测试成绩(分)如下表:
|
测试 |
第1次 |
第2次 |
第3次 |
第4次 |
第5次 |
第6次 |
第7次 |
第8次 |
|
小明 |
17 |
10 |
16 |
10 |
16 |
14 |
11 |
10 |
|
小兵 |
11 |
13 |
13 |
12 |
13 |
13 |
14 |
15 |
经统计发现两人8次测试的平均成绩相同,而又只能从两人中挑选一人去参加这个项目的比赛。当时有老师建议,可以通过考察数据中的其他信息作为参考。
(1)请根据上表中提供的数据填写下表:
|
|
平均数(分) |
众数(分) |
中位数(分) |
方差 |
|
小明 |
13 |
10 |
|
8.25 |
|
小兵 |
13 |
|
13 |
|
(2)根据以上信息,你认为当时选谁去更合适?请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com