50．由“四边形ABCD是矩形，DE平分∠ADC”知∠CDE＝∠CED＝45°，又∠BDE＝15°，所以∠CDO＝60°，由矩形的特征“对角线互相平分”可知，OD＝OC，故△OCD是等边三角形，从而有OC＝OD＝CE，∠DCO＝60°，∠OCB＝30°，进而求得∠COE＝75°．

49．因为四边形ABCD是平行四边形，所以AB//CD，

AD=BC(平行四边形的对边平行且相等)，所以∠1=∠2(两直线平行，内错角相等)，又因为AE平分∠DAB，所以∠1=∠3，所以∠2=∠3，所以DA=DE=2cm(等角对等边)．同理BC=CF=2cm．所以EF=DC-DE-CF=6 cm -2 cm -2 cm =2 cm．

48．(1)平行四边,两组对边分别相等的四边形是平行四边形;

(2)矩,有一个是直角的平行四边形是矩形.　

47．(1)因为四边形ABCD是平行四边形,所以AB=DC,又AF=CG,所以AB－AF=DC－CG,即GD=BF,又 DG∥BF,所以四边形DFBG是平行四边形,所以DF=BG;

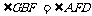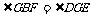　 　(2)因为四边形DFBG是平行四边形,所以DF∥GB,所以,同理可得,所以.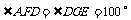　

46．因为BD=CD,所以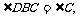又因为四边形ABCD是平行四边形,所以AD∥BC ,所以因为.　

45．如图19-4，将△BMN以∠DMN的角平分线为轴翻折至△PDM的位置，即取AD的中点P，连结PM．从而△MPD≌△NBM，故DM=MN．

44．摆放三套或四套的设计方案如图19-3所示．关键是确定这些 圆的圆心位置(圆心分别在等腰三角形和平行四边形的顶点处)，另外，设计的示意图要符合比例要求：(1)每个圆的半径为1.5㎝；(2)每个圆的圆心到方格纸外边框的距离不小于2㎝；(3)设计两圆的圆心的距离不小于3.5㎝．

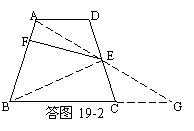
43．如图19-2，连结AE交BC的延长线于G点，连结BE．先说明△ADE≌△GCE，得到AE=GE， S_△ABG=S_梯形ABCD=2S_△ABE=2×15=30．

42．OM⊥ON，OM=ON．先说明△DCM≌△CBN得CM=BN，再推出△OCM≌△OBN得OM=ON．

41．AD⊥EF．根据有一组邻边相等的平行四边形是菱形，确定四边形AEDF是菱形，所以AD⊥EF．