
48.当CD为斜边上的高时,CD最短,从而水渠造价最价
∵CD·AB=AC·BC
∴CD=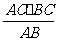 =48米
=48米
∴AD=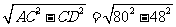 =64米
=64米
所以,D点在距A点64米的地方,水渠的造价最低,其最低造价为480元.
47.连结AE,则△ADE≌△AFE,所以AF=AD=10,DE=EF.
设CE=x,则EF=DE=8-x,BF= =6,CF=4.
=6,CF=4.
在Rt△CEF中,EF2=CE2+CF2,即(8-x)2=x2+16,故x=3
46.解:设相邻两个结点的距离为m,则此三角形三边的长分别为3m、4m、5m,
有(3m)2+(4m)2=(5m)2,
所以以3m、4m、5m为边长的三角形是直角三角形.
45.解:过点B作BC⊥AC,垂足为C.观察答图18-1可知AC=8-3+1=6,BC=2+5=7,
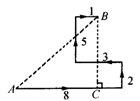
|
在Rt△ACB中,AB=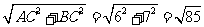 km.
km.
答:登陆点到宝藏埋藏点的直线距离是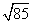 km.
km.
点拨:所求距离实际上就是AB的长.解此类题目的关键是构造直角三角形,利用勾股定理直接求解.
44.解:在Rt△ABC中,AB=4,BC=3,则有AC=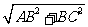 =5,
=5,
∴S△ABC=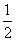 AB·BC=
AB·BC=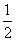 ×4×3=6.
×4×3=6.
在△ACD中,AC=5,AD=13,CD=12.
∵AC2+CD2=52+122=169,AD2=132=169,
∴AC2+CD2=AD2,∴△ACD为直角三角形,
∴S△ACD=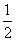 AC·CD=
AC·CD=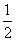 ×5×12=30,
×5×12=30,
∴S四边形ABCD= S△ABC + S△ACD =6+30=36.
43.A=81;B=64;C=100.
42.解:过点B作NM垂直于正东方向,垂足为M,则∠ABM=60°.
因为∠NBC=30°,所以∠ABC=90°.
在Rt△ABC中,AC=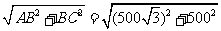 =1000(米).
=1000(米).
41.解:设BD=x,则CD=14-x,在Rt△ABD中,AD2+x2=132,
在Rt△ADC中,AD2=152-(14-x)2,
所以有132-x2=152-(14-x)2,解得x=5,
在Rt△ABD中,AD=  =12.
=12.
40.B 点拨:AB=10,∠AED=90°,CD=DE,AE=AC=6,
∴BE=4,设CD=x,则BD=8-x.
在Rt△BED中,BE2+DE2=BD2,即42+x2=(8-x)2,x=3.
39.D 点拨:AE=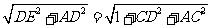
=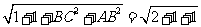 =2
=2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com