
27.(10分)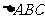 中,点
中,点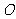 是
是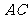 边上的一个动点,过点
边上的一个动点,过点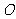 作直线
作直线 ,设交
,设交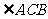 的平分线于点
的平分线于点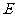 ,交
,交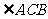 的外角平分线于点
的外角平分线于点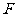 。(1)判断
。(1)判断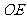 与
与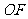 的大小关系?并说明理由;(2)当点
的大小关系?并说明理由;(2)当点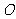 运动到何处时,四边形
运动到何处时,四边形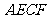 是矩形?并说出你的理由。(3)在(2)的条件下,当
是矩形?并说出你的理由。(3)在(2)的条件下,当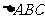 满足什么条件时,四边形
满足什么条件时,四边形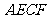 会是正方形。
会是正方形。
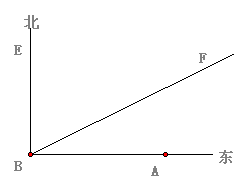
如图,A城气象台测得台风中心在A城正西方向320km的B处,以每小时40km的速度向北偏东60°的BF方向移动,距离台风中心200km的范围内是受台风影响的区域.
(1) A城是否受到这次台风的影响?为什么?
(2) 若A城受到这次台风影响,那么A城遭受这次台风影响有多长时间?
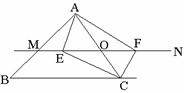
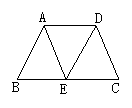
在等腰梯形ABCD中,AD∥BC,E是BC的中点,连结AE, DE, AE与DE相等吗?请说明理由.
(2) 上题中,若添加条件BC=2AD,图中有平行四边形吗?请指出来,并说明理由.
如图,A市气象站测得台风中心在A市正东方向300千米的B处,以10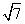 千米/时的速度向北偏西60°的BF方向移动,距台风中心200千米范围内是受台风影响的区域.
千米/时的速度向北偏西60°的BF方向移动,距台风中心200千米范围内是受台风影响的区域.
(1)A市是否会受到台风的影响?写出你的结论并给予说明;
(2)如果A市受这次台风影响,那么受台风影响的时间有多长?
如图,某货船以20海里/时的速度将一批重要物资由A处运往正西方向的B处,经小时的航行到达,到达后必须立即卸货,此时,接到气象部门通知,一台风中心正以40海里/时的速度由A向北偏西60 °方向移动,距台风中心200海里的圆形区域(包括边界)均会受到影响.
(1)问:B处是否会受到台风影响?并说明理由.
(2)为避免受到台风影响,该船应在多少小时内卸完货物?
教案题精选:
如图,在梯形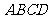 中,
中,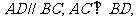 若
若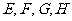 分别是梯形
分别是梯形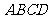 各边
各边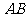 、
、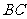 、
、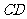 、
、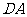 的中点。
的中点。
(1)求证:四边形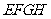 平行四边形;(2)当梯形
平行四边形;(2)当梯形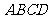 满足什么条件时,四边形
满足什么条件时,四边形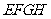 是菱形;(3)在(2)的条件下,梯形
是菱形;(3)在(2)的条件下,梯形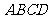 满足什么条件时,四边形
满足什么条件时,四边形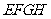 是正方形。
是正方形。
26.(10分)制作一种产品,需先将材料加热达到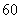 ℃后,再进行操作.设该材料温度为
℃后,再进行操作.设该材料温度为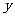 (℃),从加热开始计算的时间为
(℃),从加热开始计算的时间为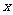 (分钟).据了解,设该材料加热时,温度
(分钟).据了解,设该材料加热时,温度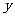 与时间
与时间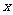 成一次函数关系;停止加热进行操作时,温度
成一次函数关系;停止加热进行操作时,温度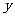 与时间
与时间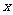 成反比例关系(如图).已知该材料在操作加工前的温度为
成反比例关系(如图).已知该材料在操作加工前的温度为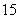 ℃,加热5分钟后温度达到
℃,加热5分钟后温度达到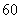 ℃.
℃.
(1)分别求出将材料加热和停止加热进行操作时,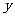 与
与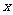 的函数关系式;
的函数关系式;
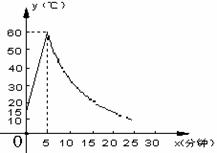 (2)根据工艺要求,当材料的温度低于
(2)根据工艺要求,当材料的温度低于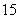 ℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
25.(10分)某校八年级学生开展踢毽子比赛活动,每班派5名学生参加.按团体总分多少排列名次,在规定时间每人踢100个以上(含100个)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个)经统计发现两班总分相等,此时有学生建议,可通过考查数据中的其他信息作为参考.请你回答下列问题:
|
|
1号 |
2号 |
3号 |
4号 |
5号 |
总分 |
|
甲班 |
100 |
98 |
110 |
89 |
103 |
500 |
|
乙班 |
86 |
100 |
98 |
119 |
97 |
500 |
(1)计算甲、乙两班的优分率;(2)求两班比赛数据的中位数。(3)估计两个比赛数据的方差哪一个小?(4)根据以上信息,你认为应该把冠军奖状发给哪一个班级?简述理由.
24.(10分)改良玉米品种后,迎春村玉米平均每公顷增加产量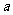 吨,原来产
吨,原来产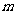 吨玉米的一块地,现在的总产量增加了
吨玉米的一块地,现在的总产量增加了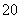 吨,原来和现在玉米的平均每公顷产量各是多少?
吨,原来和现在玉米的平均每公顷产量各是多少?
23.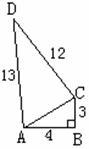 (10分)已知,如图四边形
(10分)已知,如图四边形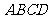 中,
中,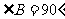 ,
,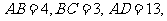
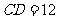 ,求:四边形
,求:四边形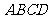 的面积.
的面积.
22. (8分)已知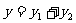 ,且
,且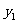 与
与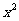 成反比例,
成反比例,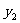 与
与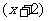 成正比例,当
成正比例,当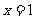 时,
时,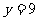 ;当
;当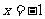 时,,
时,,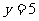 。求
。求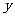 与
与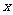 之间的函数关系式,并求当
之间的函数关系式,并求当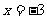 时,
时,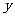 的值。
的值。
21.(每小题8分,共24分)
I.计算: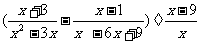 II.解分式方程:
II.解分式方程: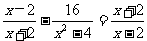
(III)如图,
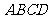 中,点
中,点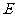 、
、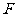 在对角线
在对角线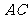 上,且
上,且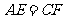 ,请你以
,请你以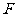 为一个端点,和图中已标明字母的某一点连成一条新线段,,猜想证明它和图中已有的某一线段相等。(只须证明一组线段即可。)
为一个端点,和图中已标明字母的某一点连成一条新线段,,猜想证明它和图中已有的某一线段相等。(只须证明一组线段即可。)
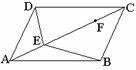 (1),连结 ;(2)猜想 = ;(3)写出证明过程。
(1),连结 ;(2)猜想 = ;(3)写出证明过程。
20.梯形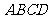 中,
中,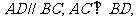 若
若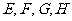 分别是梯形
分别是梯形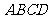 各边
各边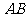 、
、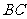 、
、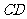 、
、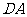 的中点。梯形
的中点。梯形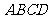 满足
条件时,四边形
满足
条件时,四边形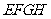 是正方形。
是正方形。
19.命题“全等三角形的面积相等”的逆命题是:
, 它是 (填入“真”或“假”)命题。
18.若样本数据1,2,3,2的平均数是a,中位数是
b,众数是c,则数据a、b、c的方差是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com