
24.解:(1)设EF=x. 依题意知:△CDE≌△CFE.
∴DE=EF=x,CF=CD=6,
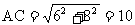
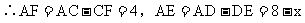

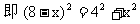 .
.
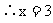
即EF=3.
(2)由(1)知:AE=8-3=5,
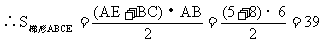 .
.
23.证明:∵四边形ABCD是正方形,AE⊥BF
∴∠DAE+∠AED = 90°,∠DAE+∠AFB = 90°
∴∠AED = ∠AFB
又∵AD = AB,∠BAD = ∠D ,
∴△AED≌△ABF
∴AE = BF
22.解:(1)平均数为5.6万元,众数为4万元,中位数为5万元.
(2)若规定平均数5.6万元为标准,则多数又无法或不可能超额完成,会挫伤员工积极性,若规定众数4万元为标准,则绝大多数人不必努力就可以超额完成,不利于提高年销售额;规定中位数5万元为标准,多数人能完成或超额完成,少数人经过努力也能完成,所以5万元标准较合理.
21.解:(1)设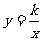
∵当x = 2时,y = 6
∴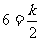
解得k = 12
∴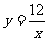
(2)把x = 4代入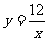 ,得
,得
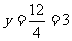
26.(12分)如图,正方形OABC的面积为16,点O为坐标原点,点B在函数y=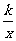 (k>0,x>0)的图象上,点P(m, n)是函数y=
(k>0,x>0)的图象上,点P(m, n)是函数y= 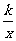 (k>0,x>0)的图象上任意一点,过点P分别作x轴、y轴的垂线,垂足分别为E、F,并设矩形OEPF和正方形OABC不重合部分的面积为S。(提示:考虑点P在点B的左侧或右侧两种情况)
(k>0,x>0)的图象上任意一点,过点P分别作x轴、y轴的垂线,垂足分别为E、F,并设矩形OEPF和正方形OABC不重合部分的面积为S。(提示:考虑点P在点B的左侧或右侧两种情况)
(1)求B点坐标和k的值;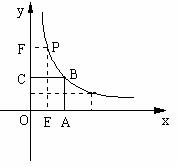
(2)当S= 8时,求点P的坐标;
(3)写出S与m的函数关系式。
附加题:画一个等腰梯形,使它的上、下底长分别为5㎝,11㎝,高为4㎝,并计算这个等腰梯形的周长和面积。
25.(10分)甲、乙两个工程队共同完成一项工程,乙队先单独做1天后,再由两队合作2天就完成了全部工程。已知甲队单独完成工程所需的天数是乙队单独完成所需天数的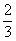 ,求甲、乙两队单独完成各需多少天?
,求甲、乙两队单独完成各需多少天?
24.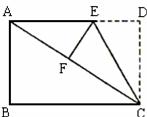 (10分)如图11,在矩形ABCD中,AB=6,BC=8.将矩形ABCD沿CE折叠后,使点D恰好落在对角线AC上的点
F处.
(10分)如图11,在矩形ABCD中,AB=6,BC=8.将矩形ABCD沿CE折叠后,使点D恰好落在对角线AC上的点
F处.
(1)求EF的长;
(2)求梯形ABCE的面积。
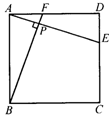
23.(8分)已知:如图,在正方形ABCD中,AE⊥BF,垂足为P,AE与CD交于点E,BF与AD交于点F,求证:AE=BF.
22.(8分)某公司10名销售员,去年完成的销售额情况如下表:
|
销售额(单位:万元) |
3 |
4 |
5 |
6 |
7 |
8 |
10 |
|
销售员人数(单位:人) |
1 |
3 |
2 |
1 |
1 |
1 |
1 |
(1)求销售额的平均数、众数、中位数;
(2)今年公司为了调动员工积极性,提高年销售额,准备采取超额有奖的措施,请根据(1)的结果,通过比较,合理确定今年每个销售员统一的销售额标准是多少万元?
21.(8分)已知y是x的反比例函数,当x = 2时, y = 6。
(1)写出y 与x 的函数关系式;
(2)求当x = 4 时y的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com