
24.在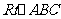 中,
中, ,
,

因为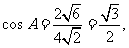 所以
所以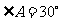 。
。
又因为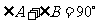 ,所以
,所以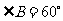
23.原式
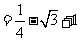

22.原式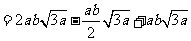
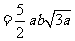
21.原式

7. 8.
8. 9.
9. 10.3 11.8,
10.3 11.8,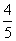
12B 13D 14D 15B 16D 17D 18A 19C 20C
1.3, 4 2.
4 2. 3.3:2,24或54 4.
3.3:2,24或54 4. 5.4 6.
5.4 6.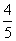







 29.如图,一个正比例函数的图象和一个一次函数的图象交于点A(-1,2),且
29.如图,一个正比例函数的图象和一个一次函数的图象交于点A(-1,2),且 的面积为5,求这两个函数的解析式。
的面积为5,求这两个函数的解析式。
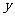
A 2
1
B -1 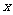
30.城市规划期间,欲拆除一电线杆AB,已知距电线杆AB水平距离14米的D 处有一大坝,背水坡CD的高度i =2:1,坝高CF=2米,在坝顶C处测得杆顶A的倾角为30º,DE之间是宽为2米的人行道,试问:在拆除电线杆AB时,为确保行人安全,是否需要将此人行道封上?试说明理由。
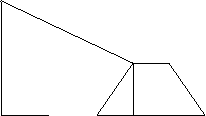
A
 30º C
30º C

人
 B 行
B 行
E 道D F
重庆市北碚区兼善中学第二学期数学期末考试
28.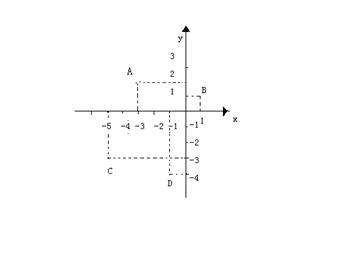 如图,学校有四栋学生宿舍,分别用A、B、C、D表示,建立如图所示的直角坐标系,四地的坐标分别为A(
如图,学校有四栋学生宿舍,分别用A、B、C、D表示,建立如图所示的直角坐标系,四地的坐标分别为A( )、B(1,1)、C(
)、B(1,1)、C( )、D(
)、D( )。为了方便学生,学校要新建一个食堂,你认为新建食堂修在哪里,对大家都方便?在图上指出食堂的具体位置和坐标。
)。为了方便学生,学校要新建一个食堂,你认为新建食堂修在哪里,对大家都方便?在图上指出食堂的具体位置和坐标。
27.在下列网格中,画四边形DEFG,使四边形DEFG∽四边形ABCD,且相似比不为1。

28.(10分)图1是边长分别为4和3的两个等边三角形纸片ABC和C′D′E′叠放在一起(C与C′重合).
(1)操作:固定△ABC,将△C′D′E′绕点C顺时针旋转30°得到△CDE,连结AD、BE,CE的延长线交AB于F(图2);
探究:在图2中,线段BE与AD之间有怎样的大小关系?试证明你的结论.
(2)操作:将图2中的△CDE,在线段CF上沿着CF方向以每秒1个单位的速度平移,平移后的△CDE设为△PQR(图3);
请问:经过多少时间,△PQR与△ABC重叠部分的面积恰好等于 ?
?
 (3)操作:图1中△C′D′E′固定,将△ABC移动,使顶点C落在C′E′的中点,边BC交D′E′于点M,边AC交D′C′于点N,设∠AC C′=α(30°<α<90,图4);
(3)操作:图1中△C′D′E′固定,将△ABC移动,使顶点C落在C′E′的中点,边BC交D′E′于点M,边AC交D′C′于点N,设∠AC C′=α(30°<α<90,图4);
探究:在图4中,线段C N·E
N·E M的值是否随α的变化而变化? 如果没有变化,请你求出
M的值是否随α的变化而变化? 如果没有变化,请你求出
 C
C N·E
N·E M的值,如果有变化,请你说明理由.
M的值,如果有变化,请你说明理由.

祝贺你做完了考题,请再仔细检查一遍,看看有没有错的、漏的,
别留下什么遗憾哦!预祝同学们暑期快乐!!!
命题人:蒋 彪 审题人:冯肖娅
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com