
解 ∵ △CAB是等腰三角形,D是底边AB的中点,
∴ AB = 2AD, CD⊥AB. 2’
在Rt△ACD中, tanA = , 3’
∴ AD = = = ≈ 1.963. 5’
∴ AB = 2AD ≈ 3.93(米). 6’
(B类题)
解 在△BCD中,∠BDC = 90°,∠B = 30°,CD = 6,
∴ BC = 2CD = 12. 3’
在△ABC中,∵ ∠ACB = 90°,
∴ cosB = . 5’
∴ AB = = = = 8. 8’
(C类题)
解 ∵ 3 (x2 + ) – 5 (x + ) – 2 = 0,
∴ x + = 或 x + = -1. 2’
由 x + = 得x = 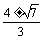 .
.
由 x + = -1得 x2 + x + 1 = 0(方程无实根)
∴ tan∠ADC = 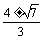 .
5’
.
5’
在Rt△ABC中, AC
= = 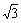 .
7’
.
7’
在Rt△ADC中, CD
= = 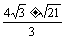 .
9’
.
9’
∵ CD < 1,
∴ CD =
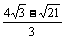 .
10’
.
10’
20.(A类题)
解 (图象略); 2’
容易求出A、B两点的坐标分别为(1,0),(5,0).AB = 4. 3’
过D作x轴的垂线,垂足为E,则E为AB的中点.
∴ AE = 2, OE = 3. 4’
∵ ⊙D切y轴于点C,连接DC,
∴ CD⊥y轴.
∴ 四边形CDEO是矩形. 5’
∴ CD = OE = 3. 即⊙D的半径等于3.
连接OD,在Rt△DOC中,由勾股定理,得OE = 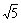 .
7’
.
7’
∴ 点C的坐标为(0,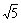 ).
8’
).
8’
(B类题)
解 设该一次函数表达式为y = kx + b,则
 3’
3’
解得 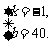 4’
4’
∴ y = - x + 40. 5’
设每件产品的销售价应定为x元,日销售利润为w元,则
w = (x – 10) (40 – x)
= - x2 + 50x – 400
= - (x – 25)2 + 225. 8’
∴ 当x = 25时,w取最大值225.
答:产品销售价定为每件25元,每日可获最大销售利润225元. 9’
(C类题)
解 (1)证明 ∵ △ABC是等腰直角三角形,O是斜边AC的中点,
∴ BO⊥AC, BO = CO = .
∴ ∠OBC =∠C. = 45° 1’
∵ PB = PD,
∴ ∠PBD =∠PDB.
∴ ∠PBO =∠PBD -∠OBC =∠PDB -∠C =∠DPE. 2’
∵ DE⊥AC,
∴ ∠PED = 90°=∠BOP. 3’
在△BPO与△PDE中,
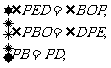
∴ △BPO ≌△PDE.
∴ BO = PE. 5’
(2)由△BPO ≌△PDE知DE = PO.
∵ △ABC是等腰直角三角形,O是斜边AC的中点,
∴ BO = CO = AO = .
则 DE = PO = a – x,BO = PE = a,OE = x. 7’
∵ S四边形PBDE = S△BPO + S梯形BOED.
∴ y =
= - 9’
自变量x的取值范围是0 < x < a. 10’
Ⅱ卷 五、21. 解(1)根据题意,得方程组
 6’
6’
解这个方程组,得
 8’
8’
∴ 这个二次函数的表达式是y = 10’
(图象略).
(2)增加的条件可以是:①抛物线上任意一点的坐标,如(1,- ),(2,-2)等;②顶点坐标为(3,- );③与x轴交于点(3+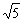 ,0)或(3-
,0)或(3-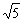 ,0);④与y轴交于点(0,2);⑤b = -3或c = 2. ……
14’
,0);④与y轴交于点(0,2);⑤b = -3或c = 2. ……
14’
评分标准:
本卷学生成绩 = 小组得分 + 个人得分.
小组得分:列对一个方程得2分,解出b、c的值各得2分,正确写出函数表达式得2分;写对应增加的条件得4分.
个人得分:根据评价栏内学生的评价内容和答卷情况,可分别记6、4、2、0分.
Ⅲ卷 六、22. 解 过B作AC的垂线,垂足为D.
在Rt△BCD中,sin∠BCD = ,
∴ BD = BC·sin∠BCD
= 142·sin75°
= 142×0.9659
≈ 137.2(米).
在Rt△ABD中,sin∠BAD = ,
∴ AB =
=
=
≈ 213(米).
根据《实践作业评价表》中学生、家长、教师的评价,参照下表计分.
|
评价人 |
评语 |
成绩 |
|||
|
优 |
良 |
中 |
不理想 |
||
|
学生本人 |
|
4-5 |
3 |
2 |
1 |
|
学生家长 |
|
4-5 |
3 |
2 |
1 |
|
任课教师 |
|
8-10 |
6-7 |
4-5 |
2-3 |
∴ ∠BCA = 15°. 2’
又 ∠BAC = 15°,
∴ BC = AB = 10. 3’
在Rt△BCE中,CE = BC·cos∠BCE
= BC·cos60°
= 10×
= 5(海里) 5’
∵ 5 > 4.8,
∴ 渔船没有进入养殖场的可能. 6’
18. 解 (1)将x = 2,y = 3代入y = x2 -2x + c,得
3 = 4 – 4 + c.
∴ c = 3. 2’
∴ 这个二次函数的表达式是y = x2 –2x +3. 3’
∵ y = x2 –2x +3 = (x –1)2 +2,
∴ 这个二次函数图象的顶点是(1,2),对称轴是x = 1. 5’
(2)当x < 1时,y随x的增大而减小. 6’
22.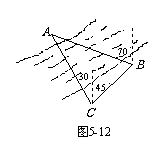 为测量河两岸A、B两点间的距离,测量人员是这样做的:如图5-12,在与点B同侧的岸边选择一点C,测得点A在点C的北偏西30°的方向,点B在点C的东北方向,在 B处测得点A在北偏西70°的方向,并量得BC = 142米. 根据这些数据,你能求出 A、B间的距离吗(精确到1米)?你还能用别的方法测量A、B间的距离吗?(测量数据长度用a、b、c表示,角度用α、β、γ表示).
为测量河两岸A、B两点间的距离,测量人员是这样做的:如图5-12,在与点B同侧的岸边选择一点C,测得点A在点C的北偏西30°的方向,点B在点C的东北方向,在 B处测得点A在北偏西70°的方向,并量得BC = 142米. 根据这些数据,你能求出 A、B间的距离吗(精确到1米)?你还能用别的方法测量A、B间的距离吗?(测量数据长度用a、b、c表示,角度用α、β、γ表示).
实践探索作业评价表
班级 姓名 交卷时间
|
评价人 |
评语 |
成绩 |
|||
|
优 |
良 |
中 |
不理想 |
||
|
学生本人 |
|
|
|
|
|
|
学生家长 |
|
|
|
|
|
|
任课教师 |
|
|
|
|
|
期中测试评价题
Ⅰ卷 一、1. 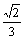 ; 2. ; 3. 2,2 -
; 2. ; 3. 2,2 -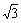 ; 4. 4;
5. 12 (
; 4. 4;
5. 12 (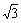 +1); 6. y = (x – 1)2 + 2; 7. x = -2; 8. 答案不唯义,如y = - x2 + x + 2,y = - 等; 9. y = x2 – 2x – 3; 10. y = x2 + 4x
+ 3.
+1); 6. y = (x – 1)2 + 2; 7. x = -2; 8. 答案不唯义,如y = - x2 + x + 2,y = - 等; 9. y = x2 – 2x – 3; 10. y = x2 + 4x
+ 3.
|
纠正错解 |
|
|
|
课后点评 |
|
|
21. 已知二次函数y = 的图象经过点A(c,-2),
已知二次函数y = 的图象经过点A(c,-2),
求证:这个二次函数图象的对称轴是x = 3.
(题目中的矩形框部分是一段被墨水污染了的无法辨认的文字).
(1)根据已知和结论中现有的信息,你能否确定问题中的二次函数的表达式?若能,请写出求解过程,并画出二次函数的图象;若不能,请说明理由.
(2)请你根据已有的信息,在原题的矩形框中,增加一个适当的条件,把原题补充完整.
小组成员、分工、评价表
Ⅲ卷 实践探索卷
(满分20分,成绩计入总分)
20.(A类8分)二次函数y = - x2 + 6x – 5的图象交x轴于A、B两点,⊙D经过A、B两点,且与y轴正半轴相切于点C. 画出二次函数y = - x2 + 6x – 5的图象,并求出点C的坐标.
(B类9分)某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
|
x(元) |
15 |
20 |
30 |
… |
|
y(件) |
25 |
20 |
10 |
… |
已知日销售量y是销售单价x的一次函数,若要使每日的销售利润最大,每件产品的销售价应定为多少元?此时日销售利润是多少?
(C类10分)如图5-11,在等腰Rt△ABC中,O是斜边AC的中点,P是斜边AC上的一个动点,D是直角边BC上的一点,且PD = PB,DE⊥AC,垂足为E.
(1)求证:PE = BO;
 (2)设AC = 2a,AP = x,四边形PBDE的面积为y,求y与x之间的函数关系式,并写出自变量x的取值范围.
(2)设AC = 2a,AP = x,四边形PBDE的面积为y,求y与x之间的函数关系式,并写出自变量x的取值范围.
Ⅱ卷 合作卷
(答卷可使用计算器,时间30分钟,满分20分,成绩计入总分)
19.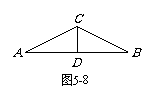 (A类6分)如图5-8,学校自行车棚的人字形屋架为等腰三角形,D是AB的中点,中柱CD = 1米,∠A = 27°. 求跨度AB(参考数据:sin27°=
0.4540,cos27°= 0.8910,tan27°= 0.5095. 精确到0.01米).
(A类6分)如图5-8,学校自行车棚的人字形屋架为等腰三角形,D是AB的中点,中柱CD = 1米,∠A = 27°. 求跨度AB(参考数据:sin27°=
0.4540,cos27°= 0.8910,tan27°= 0.5095. 精确到0.01米).
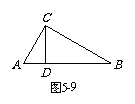 (B类8分)已知:如图5-9,在△ABC中,∠ACB = 90°,CD⊥AB,垂足为D,若∠B = 30°,CD = 6,求AB的长.
(B类8分)已知:如图5-9,在△ABC中,∠ACB = 90°,CD⊥AB,垂足为D,若∠B = 30°,CD = 6,求AB的长.
|
纠正错解 |
|
|
|
课后点评 |
|
|
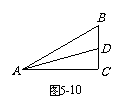 (C类10分)如图5-10,在△ABC中,∠C = 90°,∠BAC = 30°,BC = 1,D是BC边上的一点,tan∠ADC的值是方程3
(x2 + ) – 5 (x + ) = 2的一个根. 求CD的长.
(C类10分)如图5-10,在△ABC中,∠C = 90°,∠BAC = 30°,BC = 1,D是BC边上的一点,tan∠ADC的值是方程3
(x2 + ) – 5 (x + ) = 2的一个根. 求CD的长.
18.如果二次函数y = x2 -2x + c的图象经过点(2,3).
(1)求这个二次函数的表达式,并写出函数图象的顶点和对称轴;
(2)当x为何值时,y随x的增大而减小?
17. 如图5-7,一艘渔船在A处观测到东北方向有一小岛C,已知小岛C周围4.8海里范围内是水产养殖场,渔船沿北偏东30°方向航行10海里到达B处. 在B处测得小岛C在北偏东60°方向,这时渔船改变航线向正东(图中BD方向)航行,问渔船是否有进入养殖场的可能?
如图5-7,一艘渔船在A处观测到东北方向有一小岛C,已知小岛C周围4.8海里范围内是水产养殖场,渔船沿北偏东30°方向航行10海里到达B处. 在B处测得小岛C在北偏东60°方向,这时渔船改变航线向正东(图中BD方向)航行,问渔船是否有进入养殖场的可能?
16.二次函数y = ax2 +bx + c的图象如图5-6所示,则下列关于a、b、c间的关系判断正确的是( ).
 A. ab < 0 B. bc < 0 C.
a + b + c > 0 D. a
– b + c < 0
A. ab < 0 B. bc < 0 C.
a + b + c > 0 D. a
– b + c < 0

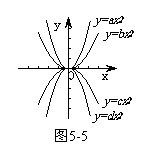
15.如图5-5,四个二次函数的图象对应的表达式分别是 y = ax2, y = bx2, y = cx2, y = dx2. 则a、b、c、d的大小关系是( );
A. d < c < b < a B. c < d < b < a
C. d < c < a < b D. c < d < a < b
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com