8．为了估计湖中有多少条鱼，先从湖中捕捉50条鱼做记号，然后放回湖里，经过一段时间，等带记号的鱼完全混于鱼群中之后，再捕捞第二次鱼共200条，有10条做了记号，则估计湖里有_____________条鱼．

7．某商品成本为500元，由于连续两年降低成本，现为190元．若每年成本降低率相同，设成本降低率为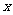，则所列方程为：　　　　　　　　　　　　　　　　 ．

6．△ABC中，已知∠C=90°，sinA=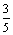，则tanA=　　　　 ．

5．菱形的一条对角线长是6cm，周长是20cm，则菱形的面积是　　　 cm²．

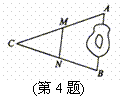
4．如图,A、B两点被池塘隔开，在AB外选一点C，连结AC和BC并分别找出其中点M、N，若测得MN＝20m，则A、B两点的距离为___________．

3．抛物线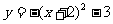的顶点坐标为 ­­­­­­­­­　　　　　　　　 .

2．任意写出一个经过二、四象限的反比例函数图象的表达式　　　　　　　 ．

1．在“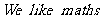．”这个句子的所有字母中，字母“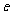”出现的频率约为　　　　 (结果保留2个有效数字)．

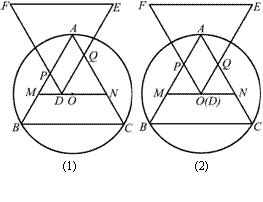
23. 如图(1)，已知⊙O是等边△ABC的外接圆，过O点作MN∥BC分别交AB、AC于M、

N，且MN=a．另一个与△ABC全等的等边△DEF的顶点D在MN上移动(不与点M、

N重合)，并始终保持EF∥BC，DF交AB于点P，DE交AC于点Q．

(1)试判断四边形APDQ的形状，并进行证明；

(2)如图⑵，当D点和圆心O重合时，请判断四边形APDQ的形状，并说明理由；你

能发现四边形APDQ的面积与△ABC的面积有何关系吗？为什么？

(3)设DM为x，四边形APDQ的面积为y，试探究y与x的函数关系式；四边形APDQ

的面积能取到最大值吗？如果能，请求出它的最大值，并确定此时D点的位置；

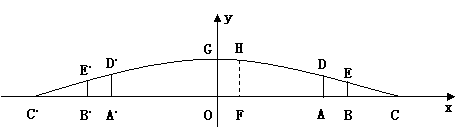如图是合肥市一处十字路口立交桥的横断面在平面直角坐标系中的示意图，横断面的地平线为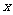轴，横断面的对称轴为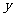轴，桥拱DGD^，部分为一段抛物线，顶点G的高度为8米，AD和A^，D^，是两侧高为5.5米的支柱，OA和为两个方向的汽车通行区，宽都为15米，线段CD和C^，D^，为两段对称的上桥斜坡，其坡度为1：4.

(1)求桥拱DGD^，所在抛物线的解析式及CC^，的长，

(2)BE和B^，E^，为支撑斜坡的立柱，其高都为4米，相应的AB和A^，B^，为两个方向的行人及非机动车通行区，试求AB和A^，B^，的宽，

(3)按规定，汽车通过该桥下时，载货最高处和桥拱之间的距离不得小于0.4米；今有一大型运货汽车，装载某大型设备后，其宽为4米，车载大型设备的顶部与地面的距离均为7米，它能否从OA(或OA^，)通过？请说明理由.