
5. 当锐角
当锐角 时,则
时,则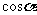 的值是( )
的值是( )
A.大于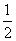 B.小于
B.小于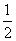 C.大于
C.大于 D.小于
D.小于
4.已知 的三边长分别为
的三边长分别为 ,
, ,2,
,2, 的两边长分别是1和
的两边长分别是1和 ,如果
,如果 ∽
∽ 相似,那么
相似,那么 的第三边长应该是 ( )
的第三边长应该是 ( )
A. B.
B. C.
C. D.
D.
3..直线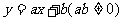 不经过第三象限,那么
不经过第三象限,那么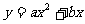 的图象大致为 ( )
的图象大致为 ( )

A. B. C. D.
2.二次函数y=x2-2x+2与y轴交点坐标为( )
A.(0,1) B.(0,2) C.(0,-1) D.(0,-2)
1.下列函数是二次函数的是( )
A. B.
B. C.
C.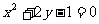 D.
D.
23、(2006河北)图14-1至图14-7的正方形霓虹灯广告牌ABCD都是20×20的等距网格(每个小方格的边长均为1个单位长),其对称中心为点O.
如图14-1,有一个边长为6个单位长的正方形EFGH的对称中心也是点O,它以每秒1个单位长的速度由起始位置向外扩大(即点O不动,正方形EFGH经过一秒由6×6扩大为8×8;再经过一秒,由8×8扩大为10×10;……),直到充满正方形ABCD,再以同样的速度逐步缩小到起始时的大小,然后一直不断地以同样速度再扩大、再缩小.
另有一个边长为6个单位长的正方形MNPQ从如图14-1所示的位置开始,以每秒1个单位长的速度,沿正方形ABCD的内侧边缘按A→B→C→D→A移动(即正方形MNPQ从点P与点A重合位置开始,先向左平移,当点Q与点B重合时,再向上平移,当点M与点C重合时,再向右平移,当点N与点D重合时,再向下平移,到达起始位置后仍继续按上述方式移动).
正方形EFGH和正方形MNPQ从如图14-1的位置同时开始运动,设运动时间为x秒,它们的重叠部分面积为y个平方单位.
(1)请你在图14-2和图14-3中分别画出x为2秒、18秒时,正方形EFGH和正方形MNPQ的位置及重叠部分(重叠部分用阴影表示),并分别写出重叠部分的面积;
(2)①如图14-4,当1≤x≤3.5时,求y与x的函数关系式;
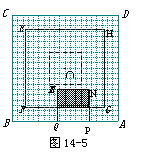
②如图14-5,当3.5≤x≤7时,求y与x的函数关系式;
③如图14-6,当7≤x≤10.5时,求y与x的函数关系式;
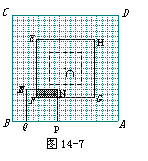
④如图14-7,当10.5≤x≤13时,求y与x的函数关系式.
(3)对于正方形MNPQ在正方形ABCD各边上移动一周的过程,请你根据重叠部分面积y的变化情况,指出y取得最大值和最小值时,相对应的x的取值情况,并指出最大值和最小值分别是多少.
 |
|||
|
|||








 |
|||||||
 |
|||||||
|
|||||||
 |
|||||||

解:(1)相应的图形如图2-1,2-2.
当x=2时,y=3;
 当x=18时,y=18.
当x=18时,y=18.
(2)①当1≤x≤3.5时,如图2-3,
延长MN交AD于K,设MN与HG交于S,MQ与FG交于T,则MK=6+x,SK=TQ=7-x,从而MS=MK-SK=2x-1,MT=MQ-TQ=6-(7-x)= x-1.
∴y=MT·MS=(x-1)(2x-1)=2x2-3x+1.
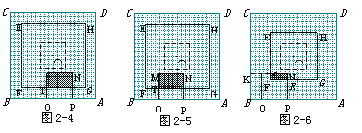
②当3.5≤x≤7时,如图2-4,设FG与MQ交于T,则
TQ=7-x,∴MT=MQ-TQ=6-(7-x)=x-1.
∴y=MN·MT=6(x-1)=6x-6.
③当7≤x≤10.5时,如图2-5,设FG与MQ交于T,则
TQ=x-7,∴MT=MQ-TQ=6-(x-7)=13-x.
∴y= MN·MT =6(13-x)=78-6x.
④当10.5≤x≤13时,如图2-6,设MN与EF交于S,NP交FG于R,延长NM交BC于K,则MK=14-x,SK=RP=x-7,
∴SM=SK-MK=2x-21,从而SN=MN-SM=27-2x,NR=NP-RP=13-x.
∴y=NR·SN=(13-x)(27-2x)=2x2-53x+351.
(3)对于正方形MNPQ,
①在AB边上移动时,当0≤x≤1及13≤x≤14时,y取得最小值0;
当x=7时,y取得最大值36.
②在BC边上移动时,当14≤x≤15及27≤x≤28时,y取得最小值0;
当x=21时,y取得最大值36.
③在CD边上移动时,当28≤x≤29及41≤x≤42时,y取得最小值0;
当x=35时,y取得最大值36.
④在DA边上移动时,当42≤x≤43及55≤x≤56时,y取得最小值0;
当x=49时,y取得最大值36.
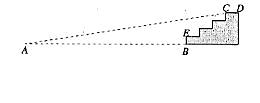
22、(2006吉林长春)某商场门前的台阶截面积如图所示。已知每级台阶的席度(如CD)均为0.3m,高度(如BE)均为0.2m。现将此台阶改造成供轮椅行走的斜坡,并且设计斜坡的倾斜角∠A为9°,计算从斜坡的起点A到台阶前点B的距离。(精确到0.1m)。
 (参考数据:
(参考数据: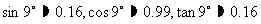 )
)
解:过C作CF⊥AB交AB的延长线于F。
由条件得CF = 0.8m,BF = 0.9m。
在Rt△CAF中,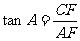 ,
,
∴ (m)。
(m)。
∴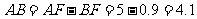 (m)。
(m)。
答:从斜坡起点A到台阶前点B的距离约为4.1m。
21、(2006福建泉州)一条隧道的截面如图所示,它的上部是一个以AD为直径的半圆O,下部是一个矩形ABCD.
⑴当AD=4米时,求隧道截面上部半圆O的面积;
⑵已知矩形ABCD相邻两边之和为8米,半圆O的半径为r米.
①求隧道截面的面积S(米2)关于半径r(米)的函数关系式(不要求写出r的取值范围);
②若2米≤CD≤3米,利用函数图象求隧道截面的面积S的最大值(π取3.14,结果精确到0.1米)

解:(1)当AD=4米时,S半圆=
=2 (米2)
(米2)
(2)①∵AD=2r,AD+CD=8
∴CD=8-AD=8-2r
∴S=
=
②由①知
又∵2米≤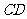 ≤3米
≤3米
∴2≤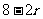 ≤3
≤3
∴2.5≤ ≤3
≤3
由①知S=
≈
=-2.43r2+16r
=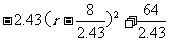
∵-2.43<0,∴函数图象为开口向下的抛物线.
∵函数对称轴 ≈3.3
≈3.3
又2.5≤ ≤3<3.3
≤3<3.3
由函数图象知,在对称轴左侧S随 的增大而增大,
的增大而增大,
故当 =3时,有S最大值.
=3时,有S最大值.

≈
=26.13
≈26.1(米2)
答:隧道截面的面积S的最大值约为26.1米2.
20、(2006湖南常德)如图,小山的顶部是一块平地,在这块平地上有一高压输电的铁架,小山的斜坡的坡度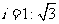 ,斜坡
,斜坡 的长是50米,在山坡的坡底
的长是50米,在山坡的坡底 处测得铁架顶端
处测得铁架顶端 的仰角为
的仰角为 ,在山坡的坡顶
,在山坡的坡顶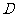 处测得铁架顶端
处测得铁架顶端 的仰角为
的仰角为 .
.
(1)求小山的高度;
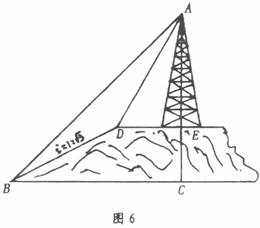
(2)求铁架的高度.( ,精确到0.1米)
,精确到0.1米)
解:(1)如图,过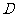 作
作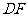 垂直于坡底的水平线
垂直于坡底的水平线 于点
于点 .
.
由已知,斜坡的坡比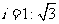 ,于是
,于是
 坡角
坡角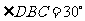
于是在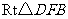 中,
中,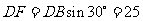
即小山高为25米
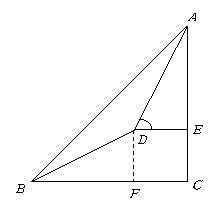 (2)设铁架的高
(2)设铁架的高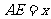 .
.
在 中,已知
中,已知 ,于是
,于是

在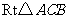 中,已知
中,已知 ,
,

又
由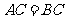 ,得
,得
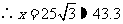 ,即铁架高
,即铁架高 米
米
19、(2006 四川资阳)如图1,已知某小区的两幢10层住宅楼间的距离为AC=30 m,由地面向上依次为第1层、第2层、…、第10层,每层高度为3 m.假设某一时刻甲楼在乙楼侧面的影长EC=h,太阳光线与水平线的夹角为α .
 (1) 用含α的式子表示h(不必指出α的取值范围);
(1) 用含α的式子表示h(不必指出α的取值范围);
(2) 当α=30°时,甲楼楼顶B点的影子落在乙楼的第几层?若α每小时增加15°,从此时起几小时后甲楼的影子刚好不影响乙楼采光 ?
解:(1)过点E作EF⊥AB于F,由题意,四边形ACEF为矩形.
∴EF=AC=30,AF=CE=h, ∠BEF=α,∴BF=3×10-h=30-h.
又 在Rt△BEF中,tan∠BEF=,
∴tanα= ,即30 - h=30tanα. ∴h=30-30tanα.
,即30 - h=30tanα. ∴h=30-30tanα.
(2)当α=30°时,h=30-30tan30°=30-30× ≈12.7,
≈12.7,
∵ 12.7÷3≈4.2, ∴ B点的影子落在乙楼的第五层 .
当B点的影子落在C处时,甲楼的影子刚好不影响乙楼采光.
此时,由AB=AC=30,知△ABC是等腰直角三角形,
∴∠ACB=45°,
∴ = 1(小时).
故经过1小时后,甲楼的影子刚好不影响乙楼采光.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com