2、二次函数y=x²-2x+2与y轴交点坐标为(　 )

A．(0，1)　 B．(0，2)　 C．(0，-1) D．(0，-2)

1、下列各式属于最简二次根式的是(　　 )。

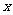31．(本题8分)如图，抛物线经过△ABC的三个顶点，已知BC∥轴，点A在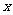轴上，点C在y轴上，且AC=BC．

　 (1)求抛物线的对称轴；

　 (2)写出A，B，C三点的坐标并求抛物线的解析式；

　 (3)探究：若点P是抛物线对称轴上且在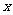轴下方的动点，是否存在△PAB是等腰三角形．

　　 若存在，求出所有符合条件的点P坐标；不存在，请说明理由．

30．(本题6分)学习投影后，小明、小颖利用灯光下自己的影子长度来测量一路灯的高度，并探究影子长度的变化规律．如图，在同一时间，身高为1．6m的小明(AB)的影子BC长是3m，而小颖(EH)刚好在路灯灯泡的正下方H点，并测得HB=6m．

　 (1)请在图中画出形成影子的光线，并确定路灯灯泡所在的位置G；

　 (2)求路灯灯泡的垂直高度GH；

　 (3)填空：如果小明沿线段BH向小颖(点H)走去，当小明走到BH中点B₁处时，则其影子B₁C₁的长为　　　 m；当小明继续走剩下路程的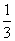到B₂处时，则其影子B₂C₂的长

　　 为　　　 m；当小明继续走剩下路程的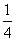到B₃处，…按此规律继续走下去，当小明

　　 走剩下路程的到处时，其影子的长为　　　　 m(直接用的代数式表示)．

29．(本题6分)如图，有一块圆形铁皮，BC是⊙O的直径，，在此圆形铁皮中剪下一个扇形(阴影部分)．

　 (1)当⊙O的半径为2时，求这个扇形(阴影部分)的面积(结果保留)．

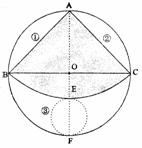　 (2)当⊙O的半径为R(R>0)时，在剩下的三块余料中，能否从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥?请说明理由．

28．(本题6分)某厂工业废气年排放量为450万立方米，为改善大气环境质量，决定分二期投入治理，使废气的年排放量减少到288万立方米，如果每期治理中废气减少的百分率相同．

　 (1)求每期减少的百分率是多少?

　 (2)预计第一期中每减少一万立方米废气需投入3万元，第二期治理中每减少一万立方米

废气需投入4．5万元，问两期治理完后共需投入多少万元?

27．(本题6分)如图，AB为⊙O的直径，弦CD⊥AB于点M，过点B作BE∥CD，交AC的延长线于点E，连结BC．　　　　　　　　　　　　　　　

(1)求证：BE为⊙O的切线；

(2)如果CD=6，tan∠BCD=，求⊙O的直径．

26．(本题6分)在直角坐标平面内，二次函数图象的顶点为A(1，一4)，且过点B(3，0)．

　 (1)求该二次函数的解析式；

　 (2)将该二次函数图象向右平移几个单位，可使平移后所得图象经过坐标原点?并直接写

出平移后所得图象与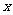轴的另一个交点的坐标．

25．(本题5分)已知关于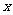的方程．

　 (1)求证：无论m取何实数值，方程有实数根．

　 (2)若等腰△ABC的一边长a=l，另两边长b，c恰好是这个方程的两根，求△ABC的周长．

24．(本题5分)如图，某幢大楼顶部有一块广告牌CD，甲乙两人分别在相距8米的A、B两处测得D点和C点的仰角分别为45°和60°，且A、B、E三点在同一水平线上，若BE=15米，求这块广告牌的高度．(计算结果保留根号)