
2.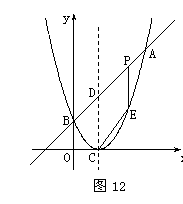 (08云南省卷24题) 24.(本大题满分14分)如图12,已知二次函数图象的顶点坐标为C(1,0),直线
(08云南省卷24题) 24.(本大题满分14分)如图12,已知二次函数图象的顶点坐标为C(1,0),直线 与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴
与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴 上.
上.
(1)求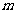 的值及这个二次函数的关系式;
的值及这个二次函数的关系式;
(2)P为线段AB上的一个动点(点P与A、B不重合),过P作 轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为
轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为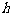 ,点P的横坐标为
,点P的横坐标为 ,求
,求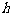 与
与 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量 的取值范围;
的取值范围;
(3)D为直线AB与这个二次函数图象对称轴的交点,在线段AB上是否存在一点P,使得四边形DCEP是平行四形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
(08云南省卷24题解析) (1) ∵ 点A(3,4)在直线y=x+m上,
∴ 4=3+m. ………………………………(1分)
∴ m=1. ………………………………(2分)
设所求二次函数的关系式为y=a(x-1)2. ………………………………(3分)
∵ 点A(3,4)在二次函数y=a(x-1)2的图象上,
∴ 4=a(3-1)2,
∴ a=1. ………………………………(4分)
∴ 所求二次函数的关系式为y=(x-1)2.
即y=x2-2x+1. ………………………………(5分)
(2) 设P、E两点的纵坐标分别为yP和yE .
∴ PE=h=yP-yE ………………………………(6分)
=(x+1)-(x2-2x+1) ………………………………(7分)
=-x2+3x. ………………………………(8分)
即h=-x2+3x (0<x<3). ………………………………(9分)
(3) 存在. ………………………………(10分)
解法1:要使四边形DCEP是平行四边形,必需有PE=DC. …………………(11分)
∵ 点D在直线y=x+1上,
∴ 点D的坐标为(1,2),
∴ -x2+3x=2 .
即x2-3x+2=0 . ………………………………(12分)
解之,得 x1=2,x2=1 (不合题意,舍去) ………………………………(13分)
∴ 当P点的坐标为(2,3)时,四边形DCEP是平行四边形. ……………(14分)
解法2:要使四边形DCEP是平行四边形,必需有BP∥CE. ………………(11分)
设直线CE的函数关系式为y=x+b.
∵ 直线CE 经过点C(1,0),
∴ 0=1+b,
∴ b=-1 .
∴ 直线CE的函数关系式为y=x-1 .
∴ 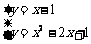 得x2-3x+2=0.
………………………………(12分)
得x2-3x+2=0.
………………………………(12分)
解之,得 x1=2,x2=1 (不合题意,舍去) ………………………………(13分)
∴ 当P点的坐标为(2,3)时,四边形DCEP是平行四边形. ……………(14分)
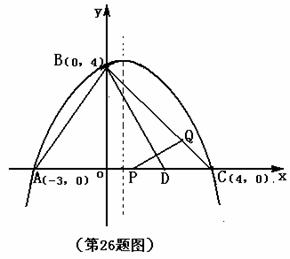
1.(08福建莆田)26.(14分)如图:抛物线经过A(-3,0)、B(0,4)、C(4,0)三点.
(1) 求抛物线的解析式.
(2)已知AD = AB(D在线段AC上),有一动点P从点A沿线段AC以每秒1个单位长度的速度移动;同时另一个动点Q以某一速度从点B沿线段BC移动,经过t 秒的移动,线段PQ被BD垂直平分,求t的值;
(3)在(2)的情况下,抛物线的对称轴上是否存在一点M,使MQ+MC的值最小?若存在,请求出点M的坐标;若不存在,请说明理由。
(注:抛物线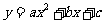 的对称轴为
的对称轴为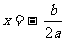 )
)
(08福建莆田26题解析)26(1)解法一:设抛物线的解析式为y = a (x +3 )(x - 4)
因为B(0,4)在抛物线上,所以4 = a ( 0 + 3 ) ( 0 - 4 )解得a= -1/3
所以抛物线解析式为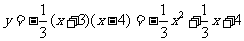
解法二:设抛物线的解析式为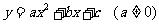 ,
,
依题意得:c=4且 解得
解得
所以 所求的抛物线的解析式为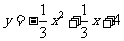
(2)连接DQ,在Rt△AOB中,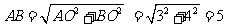
所以AD=AB= 5,AC=AD+CD=3 + 4 = 7,CD = AC - AD = 7 – 5 = 2
因为BD垂直平分PQ,所以PD=QD,PQ⊥BD,所以∠PDB=∠QDB
因为AD=AB,所以∠ABD=∠ADB,∠ABD=∠QDB,所以DQ∥AB
所以∠CQD=∠CBA。∠CDQ=∠CAB,所以△CDQ∽ △CAB
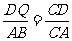 即
即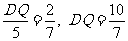
所以AP=AD
– DP = AD – DQ=5 –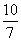 =
=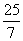 ,
,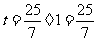
所以t的值是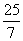
(3)答对称轴上存在一点M,使MQ+MC的值最小
理由:因为抛物线的对称轴为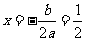
所以A(- 3,0),C(4,0)两点关于直线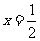 对称
对称
连接AQ交直线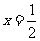 于点M,则MQ+MC的值最小
于点M,则MQ+MC的值最小
过点Q作QE⊥x轴,于E,所以∠QED=∠BOA=900
DQ∥AB,∠ BAO=∠QDE, △DQE ∽△ABO
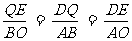 即
即 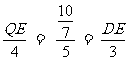
所以QE=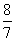 ,DE=
,DE= ,所以OE = OD + DE=2+
,所以OE = OD + DE=2+ =
=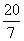 ,所以Q(
,所以Q(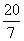 ,
,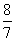 )
)
设直线AQ的解析式为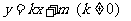
则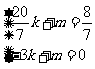 由此得
由此得 
所以直线AQ的解析式为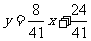 联立
联立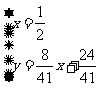
由此得 所以M
所以M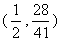
则:在对称轴上存在点M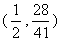 ,使MQ+MC的值最小。
,使MQ+MC的值最小。
28、(本题满分5分)传销是一种危害极大的非法商业诈骗活动,国家是明令禁止的. 参与传销活动的人,最终是要上当受骗的. 据报道,某公司利用传销活动诈骗投资人,谎称“每位投资者每投资一股450元,买到一件价值10元的商品后,另外可得到530元的回报,每一期投资到期后,若投资人继续投资,下一期追加的投资股数必须是上一期的2倍”.
退休的张大爷先投资了1股,以后每期到期时,不断追加投资,当张大爷某一期追加的投资数为16股后时,被告知该公司破产了.
(1)假设张大爷在该公司破产的前一期停止投资,他的投资回报率是多少?
(回报率= )
)
(2)试计算张大爷在参与这次传销活动中共损失了多少元钱?
27、(本题满分5分)图1是由若干个小圆圈堆成的一个形如等边三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了n层. 将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为1+2+3+…+n=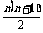 .
.
如果图1中的圆圈共有13层.
(1)我们自上往下,在每个圆圈中都图3的方式填上一串连续的正整数1,2,3,4,…,则最底层最左边这个圆圈中的数是 ;
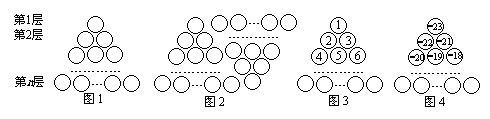 (2)我们自上往下,在每个圆圈中都图4的方式填上一串连续的整数-23,-22,-21,…,求图4中所有圆圈中各数的绝对值之和.
(2)我们自上往下,在每个圆圈中都图4的方式填上一串连续的整数-23,-22,-21,…,求图4中所有圆圈中各数的绝对值之和.
26、(本题满分10分)已知x、y为有理数,现规定一种新运算※,满足x※y=xy+1.
(1)、求2※4的值;
(2)、求(1※4)※(-2)的值;
(3)、任意选择两个有理数(至少有一个是负数),分别填入下列□和○中,并比较它们的运算结果:□※○和○※□;
(4)、探索a※(b+c)与a※b+a※c的关系,并用等式把它们表达出来.
25、(本题满分6分)已知a、b、c都是不等于0的数,求 的所有可能的值.
的所有可能的值.
24、(本题满分6分)已知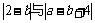 互为相反数,求
互为相反数,求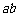 -2007的值.
-2007的值.
23、(本题满分18分)计算:
(1)-24+3.2-16-3.5+0.3
(2)0-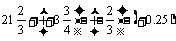
(3)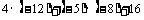 (4)
(4)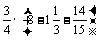
(5)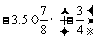 (6)
(6)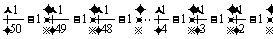
22、计算机中常用的十六进制是逢16进1的计数制,采用数字0-9和字母 A-F 共16个计数符号,这些符号与十进制的数的对应关系如下表:
|
十六进制 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
|
十进制 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
例如,用十六进制表示:E + F = 1D,则 A×B = ( )
A、 B 0 B、1A C、5F D、 6E
21、四个互不相等的整数a、b、c 、d,满足abc d=9,那么a+b+c +d的值为( )
A、0 B、4 C、9 D、不能确定
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com