
4、不解方程,判别方程5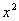 -7x+5=0的根的情况是.
-7x+5=0的根的情况是.
A.有两个相等的实数根 B.有两个不相等的实数根
C.只有一个实数根 D.没有实数根
3、化简 的结果是
的结果是
A、 B、
B、 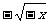 C、
C、  D、
D、 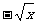
2、 实数a、b在数轴上的位置如图所示,那么化简|a-b|- 的结果是
的结果是

A.2a-b B.b C.-b D.-2a+b
1、函数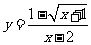 中,自变量
中,自变量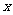 的取值范围是
的取值范围是
A. B.
B.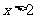 C.
C. 且
且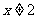 D.
D. 且
且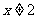
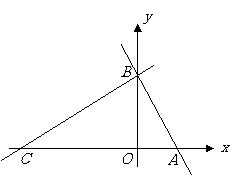
7、(2008黑龙江、鸡西、佳木斯、齐齐哈尔)如图,在平面直角坐标系中,点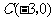 ,点
,点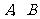 分别在
分别在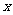 轴,
轴, 轴的正半轴上,且满足
轴的正半轴上,且满足 .
.
(1)求点 ,点
,点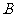 的坐标.
的坐标.
(2)若点 从
从 点出发,以每秒1个单位的速度沿射线
点出发,以每秒1个单位的速度沿射线 运动,连结
运动,连结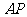 .设
.设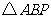 的面积为
的面积为 ,点
,点 的运动时间为
的运动时间为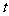 秒,求
秒,求 与
与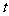 的函数关系式,并写出自变量的取值范围.
的函数关系式,并写出自变量的取值范围.
(3)在(2)的条件下,是否存在点 ,使以点
,使以点 为顶点的三角形与
为顶点的三角形与 相似?若存在,请直接写出点
相似?若存在,请直接写出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

23.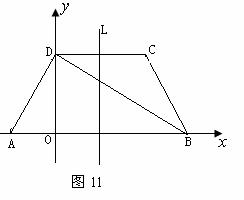 如图11所示,在梯形ABCD中,已知AB∥CD, AD⊥DB,AD=DC=CB,AB=4.以AB所在直线为
如图11所示,在梯形ABCD中,已知AB∥CD, AD⊥DB,AD=DC=CB,AB=4.以AB所在直线为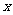 轴,过D且垂直于AB的直线为
轴,过D且垂直于AB的直线为 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(1)求∠DAB的度数及A、D、C三点的坐标;
(2)求过A、D、C三点的抛物线的解析式及其对称轴L.
(3)若P是抛物线的对称轴L上的点,那么使 PDB为等腰三角形的点P有几个?(不必求点P的坐标,只需说明理由)
PDB为等腰三角形的点P有几个?(不必求点P的坐标,只需说明理由)
6.(08广东梅州23题)
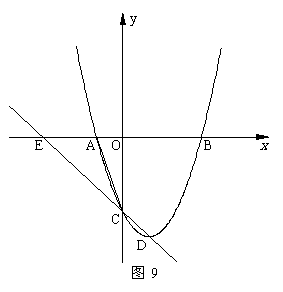
5.(08广东深圳)22.如图9,在平面直角坐标系中,二次函数 的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),
的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),
OB=OC ,tan∠ACO=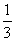 .
.
(1)求这个二次函数的表达式.
(2)经过C、D两点的直线,与x轴交于点E,在该抛物线上是否存在这样的点F,使以点A、C、E、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.
(3)若平行于x轴的直线与该抛物线交于M、N两点,且以MN为直径的圆与x轴相切,求该圆半径的长度.
 (4)如图10,若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上一动点,当点P运动到什么位置时,△APG的面积最大?求出此时P点的坐标和△APG的最大面积.
(4)如图10,若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上一动点,当点P运动到什么位置时,△APG的面积最大?求出此时P点的坐标和△APG的最大面积.
4.(08甘肃白银等9市)28.(12分)如图20,在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(4,3).平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M、N,直线m运动的时间为t(秒).
 (1) 点A的坐标是__________,点C的坐标是__________;
(1) 点A的坐标是__________,点C的坐标是__________;
(2) 当t= 秒或
秒时,MN= AC;
AC;
(3) 设△OMN的面积为S,求S与t的函数关系式;
(4) 探求(3)中得到的函数S有没有最大值?若有,求出最大值;若没有,要说明理由.
3. (08山西省卷)(本题答案见《直击中考》p28--29)26.(本题14分)如图,已知直线
(08山西省卷)(本题答案见《直击中考》p28--29)26.(本题14分)如图,已知直线 的解析式为
的解析式为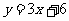 ,直线
,直线 与x轴、y轴分别相交于A、B两点,直线
与x轴、y轴分别相交于A、B两点,直线 经过B、C两点,点C的坐标为(8,0),又已知点P在x轴上从点A向点C移动,点Q在直线
经过B、C两点,点C的坐标为(8,0),又已知点P在x轴上从点A向点C移动,点Q在直线 从点C向点B移动。点P、Q同时出发,且移动的速度都为每秒1个单位长度,设移动时间为t秒(
从点C向点B移动。点P、Q同时出发,且移动的速度都为每秒1个单位长度,设移动时间为t秒(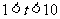 )。
)。
(1)求直线 的解析式。
的解析式。
(2)设△PCQ的面积为S,请求出S关于t的函数关系式。
(3)试探究:当t为何值时,△PCQ为等腰三角形?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com