24．(本小题满分8分)

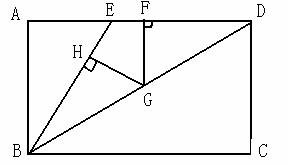
　 如图所示，在矩形ABCD中，AB=16，G在BD上，E在AD上，BE=ED，HG⊥BE于H，FG⊥AD于F。

　 (1)请猜想HG与AB－FG的关系(可不写推理过程)；

　 (2)请求出HG+FG，并写出必要的推理过程。

23．(本小题满分7分)

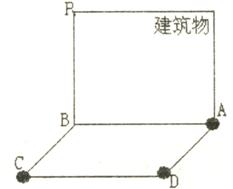
　 某地警方在一建筑物旁离地17米的P点(即PB=17米)安装了“天眼”监控器，可以清晰地观察建筑物外的矩形ABCD区域。已知AB=15米，BC=8米，此时有甲、乙、丙三个犯罪嫌疑人恰好分别在A、C、D处。

　 (1)请利用所学的知识分别求出三个犯罪嫌疑人离“天眼”的距离。(结果可以保留根号)

　 (2)指出离“天眼”最近和最远的犯罪嫌疑人分别是谁？

22．(本小题满分5分)

　 先化简，再求值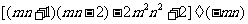：，其中，。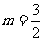

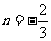21．(本小题满分6分)

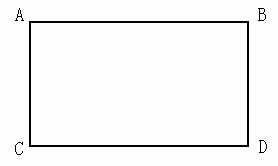　 现有一长、宽分别为3米、4米的矩形场地，要在这块矩形场地上开辟一个最大的菱形花圃，请画出其设计图，并求出其面积。

20．(本小题满分5分)

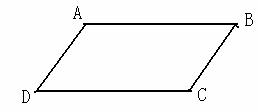
　 已知平行四边形ABCD中，AB=8，周长为24，求其余各边的长。

19．(本小题满分8分)

　 在直角△ABC中，∠C=90⁰，BC=3，AB=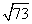，D是AC的中点，连结BD。

(1)　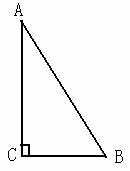　　 完善图形(直接添在图上)；

(2)　　　 求BD的长；

(3)　　　 求△ABD的面积。

18．(本小题满分6分)

　一个非零数的平方根是3a+1和a+11，求这个数的立方根。

17．(本小题满分7分，其中(1)题3分，(2)题4分)

(1)因式分解：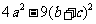

(2)计算：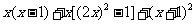

16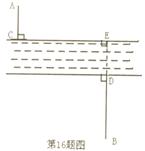．村庄A和B位于一条河流(其宽为100米)两侧，离各自的河岸距离分别是100米、200米(即AC=100米，BD=200米)，直线BD⊥CE于E，已知CE=400米。在新农村建设“村村通”工程中，计划修建一条公路和一座桥连通两村庄，若修路和建桥的单价分别是每米a元、每米b元，则当a<b时，总投入最少是___________________元。

15．我国南宋著名的数学家秦九韶(籍贯四川安岳)在其著书《数书九章》中，利用“三斜求积术”(即勾股定理等知识)十分巧妙地解决了“已知三角形的三边a、b、c，求其面积”的难题，而在此之前，西方数学家海伦(Heron)也解决了此问题，两者的数学公式分别是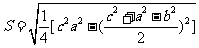(秦九韶)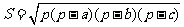，，其中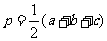(海伦)。这两个公式各有特点，若现有一个三角形，已知三边分别为5、6、7，求其面积。请你选择上面的公式，计算三角形的面积是__________。