
29. (本题满分10分)
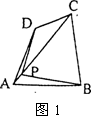
四边形一条对角线所在直线上的点,如果到这条对角线的两端点的距离不相等,但到另一对角线的两个端点的距离相等,则称这点为这个四边形的准等距点.如图l,点P为四边形ABCD对角线AC所在直线上的一点,PD=PB,PA
(本题满分10分)
四边形一条对角线所在直线上的点,如果到这条对角线的两端点的距离不相等,但到另一对角线的两个端点的距离相等,则称这点为这个四边形的准等距点.如图l,点P为四边形ABCD对角线AC所在直线上的一点,PD=PB,PA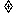 PC,则点P为四边形ABCD的准等距点.
PC,则点P为四边形ABCD的准等距点.
(1)如图2,画出菱形ABCD的一个准等距点.(1分)
(2)如图3,作出四边形ABCD的一个准等距点(尺规作图,保留作图痕迹,不要求写作法).(4分)
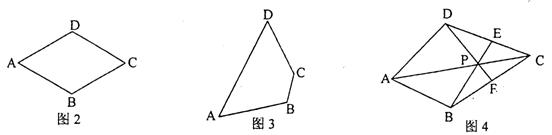
(3)如图4,在四边形ABCD中,P是AC上的点,PA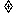 PC,延长BP交CD于点E,延长DP交BC于点F,且∠CDF=∠CBE,CE=CF.求证:点P是四边形ABCD的准等距点.(5分)
PC,延长BP交CD于点E,延长DP交BC于点F,且∠CDF=∠CBE,CE=CF.求证:点P是四边形ABCD的准等距点.(5分)
28. (本题满分10分)
如图,点
(本题满分10分)
如图,点 是等边
是等边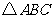 内一点,
内一点,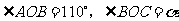 .将
.将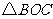 绕点
绕点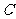 按顺时针方向旋转
按顺时针方向旋转 得
得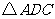 ,连接
,连接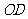 .
.
(1)求证: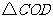 是等边三角形;(2分)
是等边三角形;(2分)
(2)当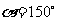 时,试判断
时,试判断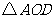 的形状,并说明理由;(3分)
的形状,并说明理由;(3分)
(3)探究:当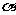 为多少度时,
为多少度时,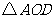 是等腰三角形?(5分)
是等腰三角形?(5分)
27. (本题满分10分) .通过市场调查,一段时间内某地区某一种农副产品的需求数量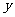 (千克)与市场价格
(千克)与市场价格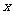 (元/千克)(
(元/千克)(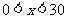 )存在下列关系:
)存在下列关系:
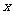 (元/千克) (元/千克) |
5 |
10 |
15 |
20 |
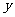 (千克) (千克) |
4500 |
4000 |
3500 |
3000 |
又假设该地区这种农副产品在这段时间内的生产数量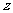 (千克)与市场价格
(千克)与市场价格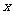 (元/千克)成正比例关系:
(元/千克)成正比例关系: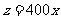 (
(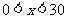 ).现不计其它因素影响,如果需求数量
).现不计其它因素影响,如果需求数量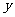 等于生产数量
等于生产数量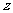 ,那么此时市场处于平衡状态.
,那么此时市场处于平衡状态.
(1)请通过描点画图探究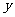 与
与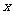 之间的函数关系,并求出函数关系式;(3分)
之间的函数关系,并求出函数关系式;(3分)


(2)根据以上市场调查,请你分析:当市场处于平衡状态时,该地区这种农副产品的市场价格与这段时间内农民的总销售收入各是多少?(3分)
(3)如果该地区农民对这种农副产品进行精加工,此时生产数量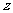 与市场价格
与市场价格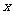 的函数关系发生改变,而需求数量
的函数关系发生改变,而需求数量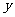 与市场价格
与市场价格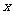 的函数关系未发生变化,那么当市场处于平衡状态时,该地区农民的总销售收入比未精加工市场平衡时增加了17600元.请问这时该农副产品的市场价格为多少元?(4分)
的函数关系未发生变化,那么当市场处于平衡状态时,该地区农民的总销售收入比未精加工市场平衡时增加了17600元.请问这时该农副产品的市场价格为多少元?(4分)
26. (本题满分9分) “今年第13号超强台风韦帕(WIPHA)18日早晨7时前后进入东海南部海面,其中心位于浙江省温岭东南方向大约490公里的东海南部海面上,即北纬24.4度,东经123.7度,中心附近最大风力有16级(55米/秒)。预计超强台风中心将以每小时20公里左右的速度向西北方向移动,逐渐向浙江沿海靠近,并可能于18日后半夜到19日上午在浙江苍南到象山一带沿海登陆,也有可能擦过浙江中北部近海北上。”以上摘自东方网9月18日消息。若现在该台风中心已至江苏沿海某城市A正南方向300千米的B处,并正沿北偏西30°方向往C处移动,且中心风力不变。当城市所受风力达到或超过四级,则称为受台风影响。(每远离台风中心20千米,风力就会减弱一级)
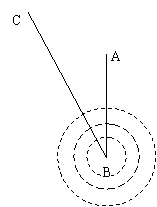 (1)该城市是否会受到台风韦帕的影响?请说明理由。
(1)该城市是否会受到台风韦帕的影响?请说明理由。
(2)若会受到影响,该城市受到台风韦帕影响的最大风力为几级?
(3)若会受到影响,那么台风影响该市的时间大约有多长?(结果保留根号)
25. (本题满分8分) 已知,如图:AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E, ∠BAC=45°给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC
∠BAC=45°给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC
④劣弧AE是劣弧DE的2倍;⑤AE=BC.
(1)其中正确结论的序号是 ;
(2)选择(1)中的一个结论,给出证明.
24. (本题满分7分) 如图所示,已知:在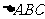 中,
中,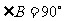 ,
,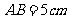 ,
,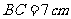 .点P从点A开始沿边AB向点B以1cm/s的速度移动,点Q从点B开始沿边BC向点C以2cm/s的速度移动.
.点P从点A开始沿边AB向点B以1cm/s的速度移动,点Q从点B开始沿边BC向点C以2cm/s的速度移动.
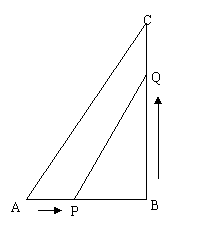 (1) 如果P、Q分别从A,B同时出发,那么几秒后,
(1) 如果P、Q分别从A,B同时出发,那么几秒后,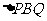 的面积等于
的面积等于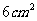 ?
?
(2)在 (1)中,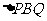 的面积能否等于
的面积能否等于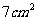 ?说明理由.
?说明理由.
23. (本题满分8分) 观察下列各式及验证过程:
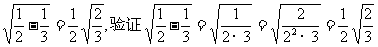 ;
;
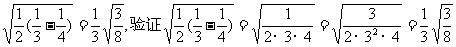
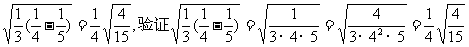
(1)按照上述三个等式及其验证过程中的基本思想,猜想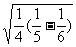 的变形结果并进行验证。
的变形结果并进行验证。
(2)针对上述各式反映的规律,写出用n(n为任意的自然数,且n≥2)表示的等式,并给出证明。
22.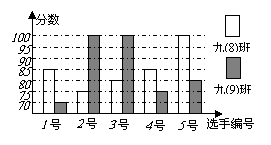 (本题满分8分) 某中学为迎接“十七”大,将开展“祖国在我心中”演讲比赛活动。九(8)、九(9)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示。
(本题满分8分) 某中学为迎接“十七”大,将开展“祖国在我心中”演讲比赛活动。九(8)、九(9)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示。
(1)根据右图填写下表;(4分)
|
|
极差(分) |
平均分(分) |
中位数(分) |
众数(分) |
|
九(8)班 |
|
|
|
|
|
九(9)班 |
|
|
|
|
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好?(2分)
(3)如果在每班参加复赛的选手中分别选出2人参加决赛,你认为哪个班的实力更强一些,说明理由。(2分)
21. (本题满分8分) 已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.
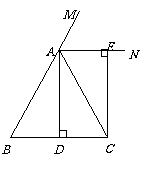 (1)求证:四边形ADCE为矩形;
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
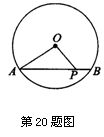
20. 如图,⊙O的直径为10,弦AB=8,P是弦AB上的一个动点,那么OP长度的取值范围是


第14题 第19题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com