
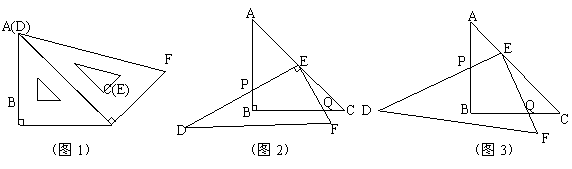
28.如图1,直角三角板ABC和直角三角板DEF满足AB=BC,AC=DE,∠ABC=∠DEF=90°,∠EDF=30°.
[操作]将三角板DEF的直角顶点E放置于三角板ABC的斜边AC上(不与A、C两点重合),再将三角板DEF绕点E旋转,并使边DE与边AB交于点P,边EF与边BC于点Q.
[探究]在旋转过程中,
(1)如图2,当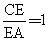 时,EP与EQ满足怎样的数量关系?并给出证明;
时,EP与EQ满足怎样的数量关系?并给出证明;
(2)如图3,当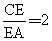 时EP与EQ满足怎样的数量关系?,并说明理由;
时EP与EQ满足怎样的数量关系?,并说明理由;
(3)根据你对(1)、(2)的探究结果,试写出当时,EP与EQ满足的数量关系式为_________,其中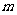 的取值范围是_______(直接写出结论,不必证明). (12分)
的取值范围是_______(直接写出结论,不必证明). (12分)
 |
|||
|
|||
27.(1)探究新知:
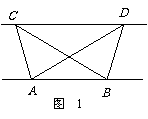
如图1,已知△ABC与△ABD的面积相等,
试判断AB与CD的位置关系,并说明理由.
(2)结论应用:
 ① 如图2,点M,N在反比例函数
① 如图2,点M,N在反比例函数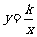 (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.
试证明:MN∥EF.
② 若①中的其它条件不变,只改变点M,N的位置,如图3所示,请判断MN与EF是否平行?并说明理由.(12分)
26.因市场需要,某企业生产一批童装需甲种布料2400米和乙种布料1200米.
(1)已知该企业安排140人生产这两种布料,每人每天能生产甲种布料30米或乙种布料20米.问:应怎样安排才能使他们同时完成任务?
(2)若计划用这批布料生产A、B两种款式的童装共4000套,已知两种童装的用料和单件利润如下表:
|
服装款式 |
甲种布料 |
乙种布料 |
单件利润 |
|
A |
0.54米 |
0.26米 |
40元 |
|
B |
0.78米 |
0.41米 |
50元 |
|
服装款式 |
甲种布料 |
乙种布料 |
单件利润 |
|
A |
0.54米 |
0.26米 |
40元 |
|
B |
0.78米 |
0.41米 |
50元 |
|
服装款式 |
甲种布料 |
乙种布料 |
单件利润 |
|
A |
0.54米 |
0.26米 |
40元 |
|
B |
0.78米 |
0.41米 |
50元 |
问:这4000套童装最多能获得多少利润?(10分)
|
服装款式 |
甲种布料 |
乙种布料 |
单件利润 |
|
A |
0.54米 |
0.26米 |
40元 |
|
B |
0.78米 |
0.41米 |
50元 |
25. 先观察下列等式,然后用你发现的规律解答下列问题.
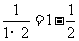
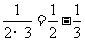
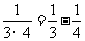
……
(1) 计算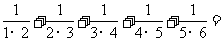 ;
;
(2) 探究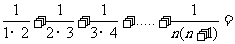 ;(用含有
;(用含有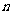 的式子表示)
的式子表示)
(3)若 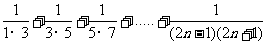 的值为
的值为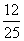 ,求
,求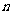 的值(10分).
的值(10分).
24.如图,在同一个坐标系中,双曲线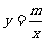 与直线y=kx+b相交于A(-3,1)、B两点,B点的横坐标为2,直线AB分别交x轴、y轴于D、C两点.
与直线y=kx+b相交于A(-3,1)、B两点,B点的横坐标为2,直线AB分别交x轴、y轴于D、C两点.
(1)求出这两个函数的解析式;并在下面的平面直角坐标系中画出简图;
(2)求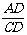 的值;
的值;
(3)观察图象并回答:当x取什么值时,反比例函数值大于一次函数的值?(10分)

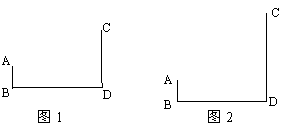
23.如下图1所示:AB⊥BD于点B,CD⊥BD于点D.
(1)在BD上找一点P使△ABP∽△CDP,请作出P点(不写作法,保留作图痕迹);
(2)如下图2所示,若AB=1,BD=4,CD=4.在BD上是否存在点P,使以C、D、P为顶点的三角形与P、B、A为顶点的三角形相似?若存在求出BP的长;若不存在请说明理由.
(10分)
|
22.如图,点P是线段AB的黄金分割点,且PA>PB.
 (1)线段PA、PB、AB之间应满足的关系是
;
(1)线段PA、PB、AB之间应满足的关系是
;
(2)若AB=8,则PB≈ (精确到0.01);
(3)若以PA为边的正方形的面积为S1,而以AB、PB为邻边的长方形的面积为S2,则S1与S2的大小关系是什么? (8分)
21.解方程:(1) (4分) (2)
(4分) (2)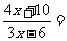
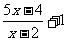 (4分)
(4分)
20.(1) 解不等式: 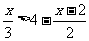 (4分) (2) 解不等式组:
(4分) (2) 解不等式组: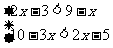 (4分)
(4分)
19.(1)计算:1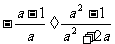 (4分)
(4分)
(2)先化简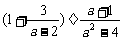 , 然后请再从0,-2 , 2中选择一个合适的数代入,求出这个代数式的值。(4分)
, 然后请再从0,-2 , 2中选择一个合适的数代入,求出这个代数式的值。(4分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com