
5、写出一个分子至少含有两项,且能够约分的分式______________.
|
学生 |
投进球数 |
没投进球数 |
投进次数 |
|
甲 |
10 |
5 |
15 |
|
乙 |
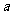 |
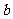 |
18 |
4、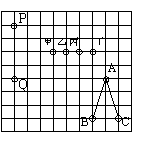 如图所示,棋盘上有A、B、C三个黑子与P、Q两个白子,要使△ABC ∽△RPQ,则第三个白子R应放的位置可以是 ______.(答案填:“甲、乙、丙、丁”)
如图所示,棋盘上有A、B、C三个黑子与P、Q两个白子,要使△ABC ∽△RPQ,则第三个白子R应放的位置可以是 ______.(答案填:“甲、乙、丙、丁”)
3、甲、乙两人比赛射击,两人所得的平均环数相同,其中甲所得的环数的方差为5,乙所得的环数如下:5、6、9、10、5,则这两人中成绩较为稳定的是_____.(填“甲”或“乙”)
2、分解因式: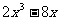 =_____________.
=_____________.
1、不等式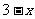 <
<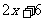 的解集是___________.
的解集是___________.
24、(12分)甲、乙两人玩“锤子、石头、剪子、布”游戏,他们在不透明的袋子中放入形状、大小均相同的15张卡片,其中写有“锤子”、“石头”、“剪子”、“布”的卡片张数分别为2,3,4,6。两人各随机摸出一张卡片(先摸者不放回)来比胜负,并约定:“锤子”胜“石头”和“剪子”,“石头”胜“剪子”,“剪子”胜“布”,“布”胜“锤子”和“石头”,同种卡片不分胜负。
(1)若甲先摸,则他摸出“石头”的概率是多少?
(2)若甲先摸出了“石头”,则乙获胜的概率是多少?
(3)若甲先摸,则他先摸出哪种卡片获胜的可能性最大?
23、(10分)如图,已知反比例函数 的图象与一次函数
的图象与一次函数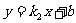 的图象交于A、B两点, A(2,n),B(-1,-2) .(1)求反比例函数和一次函数的关系式;(2)试证明线段AB分别与x轴、y轴分成三等分.⑶利用图象直接写出不等式
的图象交于A、B两点, A(2,n),B(-1,-2) .(1)求反比例函数和一次函数的关系式;(2)试证明线段AB分别与x轴、y轴分成三等分.⑶利用图象直接写出不等式
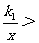 k
k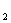 x+b的解集
x+b的解集
22、(10分)如图:已知△ABC中,AB=5,BC=3,AC=4,PQ∥AB,P点在AC上(与A、C不重合),Q在BC上.
(1) 当△PQC的面积是四边形PABQ的面积 时,求CP的长.
时,求CP的长.
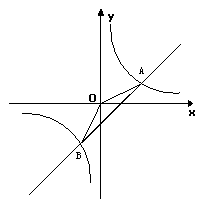 (2)当△PQC的周长与四边形PABQ的周长相等时,求CP的长.
(2)当△PQC的周长与四边形PABQ的周长相等时,求CP的长.

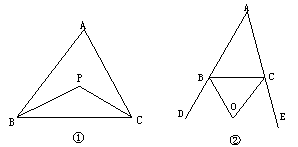
21、(10分)⑴如图①,在△ABC中, P是△ABC内任意一点,∠BPC与∠A有怎样的大小关系?证明你的结论。⑵①如图②,△ABC两个外角∠CBD、∠BCE的角平分线相交于点O,∠A=40°,求∠BOC的度数。②已知∠A=n°,求∠BOC的度数。
20、(10分)某公司在工程招标时,接到甲、乙两个工程队的投标书.每施工一天,需付甲工程队工程款1.5万元,付乙工程队工程款1.1万元,工程领导小组根据甲、乙两队的投标书测算,形成下列三种施工方案:
①甲队单独完成此项工程刚好如期完工;②乙队单独完成此项工程要比规定工期多用5天;③若甲、乙两队合作4天,剩下的工程由乙队独做也正好如期完工;
如果工程不能按预定时间完工,公司每天将损失3000元,你觉得哪一种施工方案最节省工程款,并说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com