
7.一组数据中有一个数据发生改变,则下列说法正确的是
A.众数一定会跟着变
B.中位数一定会跟着变
C.平均数一定会跟着变
D.平均数、中位数和众数都有可能不变
6. 如图是甲、乙两户居民家庭全年支出费用的扇形统计图,下面对全年食品支出费用判断正确的是
如图是甲、乙两户居民家庭全年支出费用的扇形统计图,下面对全年食品支出费用判断正确的是
A.甲户比乙户多
B.乙户比甲户多
C.甲、乙两户一样多
D.无法确定哪一户多
5.如图,身高1.6m的学生想测量学校旗杆的高度,当他站在C处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2.0m,BC=8.0m,则旗杆的高度是
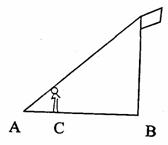 A.6.4m
A.6.4m
B.7.0m
C.8.0m
D.9.0m
4.如图:AB∥DE,CD=BF,若△ABC≌△EDF,还需补充的条件可以是
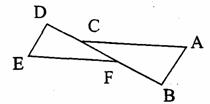 A.∠B=∠E
A.∠B=∠E
B.AC=EF
C.AB=ED
D.不用补充条件
3.直线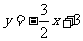 与x轴、y轴所围成的三角形的面积为
与x轴、y轴所围成的三角形的面积为
A.3
B.6 C.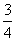 D.
D.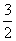
2.函数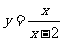 的自变量x的取值范围是
的自变量x的取值范围是
A.x≠-2 B.x≠2 C.x>2 D.x<2
1.分式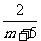 的值为1时,m的值是
的值为1时,m的值是
A.2 B.-2 C.-3 D.3
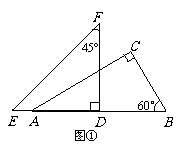
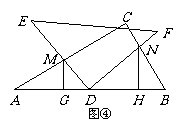
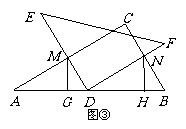
28、已知:将一副三角板(Rt△ABC和Rt△DEF)如图①摆放,点E、A、D、B在一条直线上,且D是AB的中点。. 将Rt△DEF绕点D顺时针方向旋转角α(0°<α<90°),在旋转过程中,直线DE、AC相交于点M,直线DF、BC相交于点N,分别过点M、N作直线AB的垂线,垂足为G、H。.
 (1)当α=30°时(如图②),求证:AG=DH;
(1)当α=30°时(如图②),求证:AG=DH;
(2)当α=60°时(如图③),(1)中的结论是否成立?请写出你的结论,并说明理由;
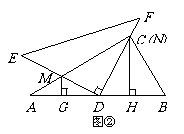
 (3)当0°<α<90°时,(1)中的结论是否成立?请写出你的结论,并根据图④说明理由
(3)当0°<α<90°时,(1)中的结论是否成立?请写出你的结论,并根据图④说明理由。. (12分)

2008-2009学年度第二学期期终考试
八年级数学试卷参考答案
一.开心选一选,表现出你的能力(每小题3分,计24分)
1.D 2.D 3.C 4.B 5.D 6.B 7.A 8.A
二、静心填一填,你一定能行(每题3分,共30分)
9. 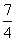 10. 5 11. 相等的角都是直角 12. 答案不唯一,如
10. 5 11. 相等的角都是直角 12. 答案不唯一,如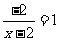 13. 25 14. 13 15. x<2 16. 3.09
17. 18 18.
13. 25 14. 13 15. x<2 16. 3.09
17. 18 18. 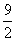
三.潜心解一解,你一定会成功(8分×4+10分×4+12分×2=96分)
19. (1)由不等式(1)得a<3 由不等式(2)得a≥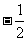 3 ′
∴不等式组的解集为
3 ′
∴不等式组的解集为 ≤a<3 4′
≤a<3 4′
(2)化简为a-4 2 ′ 满足条件的a为1. 3′ 所以原式=-3 4′
20. ①x=5 3′ 检验x=5时(x-1)(x+1)≠0 ∴x=5是原方程的解 4′
②x=2 3′检验x=2时x-2=0 ∴x=2是原方程的增根. 原方程无解. 4′
21. (1) C的坐标是(6 ,-4 ) 2′
(2)图略。C,的坐标(-3 ,2 ) 6′
(3)D,的坐标(-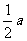 ,-
,-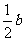 ) 8′
) 8′
22.(1)AE= 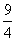 4′ (2)DP=8 8′
4′ (2)DP=8 8′
23. 略。(1) 6′ (2)10′
24. (1)y=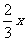 y=
y= 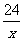 6′
6′
(2) 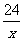 <1.6得x>15
9′
<1.6得x>15
9′
答 略。 10′
25. (1) 25×200×5+200×50=35000 元 4′ (2) 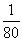 7′ (3)
7′ (3) 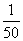 10′
10′
26. 解:(1) ∵AB=14, BD=7,BC=28, ∴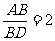
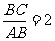 ∴
∴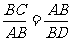 又∵∠B=∠B ∴△ABD∽△CBA
∴∠BAD=∠C 而∠BAD=∠EAC ∴∠EAC=∠C ∴CE=AE=12 3′
又∵∠B=∠B ∴△ABD∽△CBA
∴∠BAD=∠C 而∠BAD=∠EAC ∴∠EAC=∠C ∴CE=AE=12 3′
(2) ∵AB=14,AE=12,BD=7,BC=28,CE=12 ∴DE=9,BE=16
∴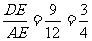
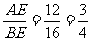 ∴
∴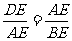
又∵∠AED=∠AEB ∴ △AED∽△BEA 7′
(3) ∵△AED∽△BEA ∴∠DAE=∠B 又∵∠BAD=∠EAC ∴∠CAD=∠ADC ∴AC=CD=9+12=21 10′
27.解:(1)设直线OM的函数关系式为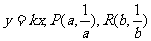 .
.
则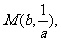 ∴
∴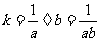 .
.
∴直线OM的函数关系式为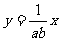 5′
5′
(2)∵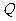 的坐标
的坐标 满足
满足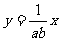 ,∴点
,∴点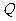 在直线OM上.6′
在直线OM上.6′
∵四边形PQRM是矩形,∴SP=SQ=SR=SM= PR.
PR.
∴∠SQR=∠SRQ.
∵PR=2OP,∴PS=OP= PR.
PR.
∴∠POS=∠PSO. 8′
∵∠PSQ是△SQR的一个外角,
∴∠PSQ=2∠SQR.
∴∠POS=2∠SQR. 10′
∵QR∥OB,
∴∠SOB=∠SQR.
∴∠POS=2∠SOB.
∴∠SOB=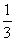 ∠AOB.
12′
∠AOB.
12′
28. (1)∵∠A=∠ADM=30° ∴AM=MD
∵∠BDC=90°-∠ADM=60°= ∠B ∴BC=BD=CD
∵MG⊥AD NH⊥BD
∴AG= AD DH=
AD DH= BD
BD
∵AD=BD ∴AG=DH 4′
(2)结论成立 5′
∵∠ADM=60° ∴∠BDN=30°
在Rt△AMD和△DBN中
∵∠ADM=∠B AD=BD ∠A=∠BDN
∴△AMD≌△DNB ∴AM=DN
∵MG⊥AD NH⊥BD ∴△AMG≌△DNH ∴AG=DH 8′
(3)结论成立 9′
∵Rt△AMG∽Rt△NBH Rt△DMG∽Rt△NDH
∴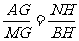
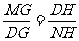
∴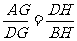 ∴
∴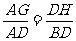
∵AD=BD
∴AG=DH 12′
27.“三等分角”是数学史上一个著名问题,但仅用尺规是不可能“三等分角”的 .下面是数学家帕普斯借助函数给出的一种“三等分锐角“的方法(如图),将给定的锐角∠AOB置于直角坐标系中,使角的顶点与坐标原点O重合,边OB在x轴上、边OA与函数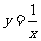 的图象交于点P,以P为圆心,以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到得到∠MOB,则
的图象交于点P,以P为圆心,以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到得到∠MOB,则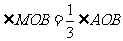 .要明白帕普斯的方法,请你研究以下问题:
.要明白帕普斯的方法,请你研究以下问题:
(1)设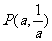 、
、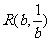 ,求直线OM相对应的函数解析式(用含a,b的代数式表示).
,求直线OM相对应的函数解析式(用含a,b的代数式表示).
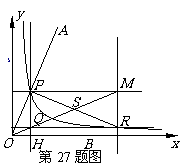 (2)分别过P和R作y轴和x轴的平行线,两直线相交于点Q,请说明Q点在直线OM上,据此证明
(2)分别过P和R作y轴和x轴的平行线,两直线相交于点Q,请说明Q点在直线OM上,据此证明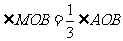 .(
.(1012分)
26、在△ABC中,AB=14,AE=12,BD=7,BC=28,且∠BAD=∠EAC.
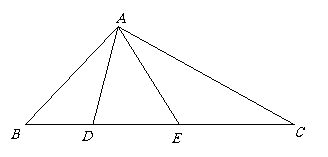 (1)求EC的长;
(1)求EC的长;
(2)请判断一下:求证:△AED∽与△BEA是否相似?并说明理由.
(3)(2)求AC的长.(10分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com