(一)本章知识结构框图

(二)重视分式与实际的联系，体现数学建模思想

由于分式是在分数基础上再次抽象的产物，所以相对说来就与客观实际的联系而言，分式不如分数更直接。但是，如果我们不仅考虑实际问题中的具体数值，而且考虑其中的运算或对应规律，那么仍然有与分式存在密切联系的实际问题情景。

如前所述，本章教科书中从引言开始安排了大量实际问题，一方面要体现与研究分数类似研究分式同样也是实际需要，另一方面也是为通过运用分式为工具分析与解决实际问题，提高学生把实际问题转化为数学形式的能力，即结合本章内容体现数学建模思想，进一步加强学生应用数学知识于实际问题的兴趣和意识，从长远看这将有助于培养学生的创新精神。

在本章的教学和学习中，应重视分式与实际的联系，选择一些适合分式内容而又接近学生生活的实际问题，结合这些问题展开分式的内容。要注意避免脱离任何实际问题地讲述分式的内容，虽然这种纯数学的处理方法在数学体系内部并无问题，但是从教学角度看它具有局限性，不适合初中学生接受，也不利于全面地提高学生素质。总之，要充分注意有关现实背景，通过它们反映出分式来自实际又服务于实际，加强对代数式(包含分式)也是解决现实问题的一种数学模型的认识。

对于把实际问题转化为有关代数式的问题，分析和解决它们的关键是找出问题中相关数量之间的运算关系，并把这样的关系 “翻译”为数学形式，而正确地理解问题情境是基础。在本章的教学和学习中，可以从多种角度思考实际问题，例如借助图象、表格、式子等进行分析，发现其中的数量关系，并检验所建立的式子的合理性。

(一)重视分数与分式的联系，注意通过分数认识分式

数学是以数量关系和空间形式为主要研究对象的科学，数量关系和空间形式是从现实世界中抽象出来的，这样的抽象是一个逐步深入的过程。人们首先从计算具体物体个数的活动中抽象出整数的概念，又从把一个具体物体分为若干份的活动中抽象出分数的概念，这是一种从实物到数的抽象。人们在研究整数和分数的过程中，为了更好地反映一般规律，又抽象出整式和分式的概念，这是一种从数到式的抽象。

正如前面所述，分数与分式的关系是具体与抽象、特殊与一般的关系，即相对于分式而言分数就是具体的、特殊的基础对象。分式是把具体的分数一般化后的抽象代表，根据这种关系，分式的基本性质、约分与通分、四则运算法则等应该与分数的基本性质、约分与通分、四则运算法则等相对应，即两者具有一致性，这也可以说是数式通性。“从具体到抽象，从特殊到一般”，是人们认识事物往往经历的过程，本章教科书对分式的概念、基本性质、约分与通分、四则运算法则等内容的展开，充分地考虑了这样的认识过程。因此，教学中应重视分数与分式的联系，考虑到学生对分数已有一定认识的基础，要发挥这样的认识基础的作用，通过分式与分数的类比，从具体到抽象、从特殊到一般地认识分式，这将有助于理解和记忆所学的分式内容。同时，这样的学习过程对于培养良好的学习方法也会起到引导作用。

(三)分析分式方程的特点，明确指出解分式方程的基本思路

在学习本章之前，学生已经分两次学习过整式方程(一元一次方程、二元一次方程组)，他们对于整式方程特别是一元一次方程的解法及其基本思路(使方程逐步化为的形式)已经比较熟悉。分式方程的未知数在分母中，它的解法比以前学过的方程复杂，随着问题复杂性的增加，人们需要不断地提高认识问题的水平，这里包括提高对新事物与已熟悉的事物之间的联系的认识。这种认识水平的提高，是构建知识体系的过程中不可缺少的。

本章最后的第16．3节“分式方程”，从分析分式方程的特点入手，引出解分式方程的基本思路，即通过去分母使分式方程化为整式方程，再解出未知数。教科书注意在这里要体现出解分式方程的基本思路是很自然、很合理地产生的，是在原来已经认识的解方程的基本思路──使方程逐步化为 的形式的想法基础上发展而得到的。这样处理既突出了分式方程解法上的特点及其算理，又反映了分式方程与整式方程在解法上的内在联系。

在强调解分式方程必须检验时，考虑到学生的知识基础和接受能力，教科书没有对解分式方程中增根的理论问题进行深入的讨论，而是通过具体例子展现了解分式方程时可能出现增根的现象，并结合例子分析了什么情况下产生增根，然后归纳出检验增根的方法，这样处理是想以典型例子简明地说明检验增根方法的依据。教科书的编者对如何把握这个问题的深度作了认真思考，力求做到既说明做法的合理性，有适可而止，不超越学生的实际水平。

在本章小结中，教科书通过本章知识结构图和思考题，再次强调了解分式方程的基本思路以及检验的问题，这又一次反映出编者对分式方程不仅关注使学生会解，而且还重视使学生认识解法后面的道理，即使学生能知其然也知所以然。

(二)通过类比分数，从具体到抽象、从特殊到一般地认识分式

人们认识事物往往经历“从具体到抽象，从特殊到一般”的过程，本章教科书对几个内容的安排正是按照这样的过程展现的。

分数与分式的关系是具体与抽象、特殊与一般的关系。分数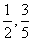等表示具体的数值，或者说每个分数表示两个特殊的整数的除法；分式则具有一般的、抽象的意义，例如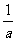表示的是一般的倒数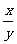，表示的是任意两个数的除法(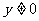)。分式的概念、基本性质、约分与通分、四则运算法则，是从分数的概念、基本性质、约分与通分、四则运算法则中经过再抽象而产生的。在学习本章之前，学生已经对分数有较多的了解，因此本章教科书的另一个编写特点是：在学生对分数已有认识的基础上，通过分式与分数的类比，从具体到抽象、从特殊到一般地认识分式。在16．1节讨论分式的基本性质、约分、通分和11．2节讨论分式的四则运算时，教科书通过多次的“观察”“思考”，进行上述类比，温故而知新，完成知识的深化。希望读者能细心体会这样安排的良苦用心，教学中充分发挥知识之间正向迁移的积极作用。

(一)反映分式和分式方程等概念的实际背景，体现数学概念来自实际、服务于实际

本章在引出分式的概念之前，安排了“思考”如何用式子表示实际问题中的数量关系；在讨论分式的乘除和加减的过程中，前后安排了涉及容积、工作效率、耕作面积、工程进度、增长率等多个实际问题；在讨论分式方程时，更注意结合分析、解决实际问题逐步深入。可以看出，本章从引言到小结始终保持贴近实际、贴近生活。这样编写的目的主要是反映两重意思：

1、客观世界中有大量的问题需要用数学进行研究，许多数学概念正是在客观实际的需求中产生的；

2、掌握数学知识和方法后，可以能动地运用它们分析和解决大量的实际问题。

上述两方面是符合辩证唯物主义关于理论与实际的关系的观点的，在本套教科书的其他部分也有这样的反映。

人们接受正确的哲学观点需要经历不断加深认识的过程，结合学习的不同阶段渗透辩证唯物主义和历史唯物主义，帮助学生逐步形成正确的世界观和方法论，是数学教育的任务之一。本套教科书力求体现的一个特点，就是使它成为反映科学发展和文化进步的一面镜子，使学生通过这面镜子的照射更清楚地认识数学的本来面目、更清楚地认识世界。

本章中安排大量实际问题，也是为更好地体现本套教科书非常重视的一点，即通过分析与解决实际问题，提高学生联系实际地应用数学知识的意识、兴趣和能力，更好地培养他们的创新精神。

(四)课时安排

本章教学时间约需13课时，具体分配如下(仅供参考)：

16．1　 分式　　　　　　　　　　　　　　　　　　　　　　　　 2课时

16．2　 分式的运算　　　　　　　　　　　　　　　　　　　　　 6课时

16．3　 分式方程　　　　　　　　　　　　　　　　　　　　　　 3课时

数学活动

小结　　　　　　　　　　　　　　　　　　　　　　　　　　　　 2课时

(三)课程学习目标

本章教科书的设计与编写以下列目标为出发点：

1、以描述实际问题中的数量关系为背景，抽象出分式的概念，体会分式是刻画现实世界中数量关系的一类代数式。

2、类比分数的基本性质，了解分式的基本性质，掌握分式的约分和通分法则。

3、类比分数的四则运算法则，探究分式的四则运算，掌握这些法则。

4、结合分式的运算，将指数的讨论范围从正整数扩大到全体整数，构建和发展相互联系的知识体系。

5、结合分析和解决实际问题，讨论可以化为一元一次方程的分式方程，掌握这种方程的解法，体会解方程中的化归思想。