
3、通过具体的例子,了解定理的含义,了解逆命题、逆定理的概念,知道原命题成立其逆命题不一定成立。
2、 会运用勾股定理的逆定理判定直角三角形;
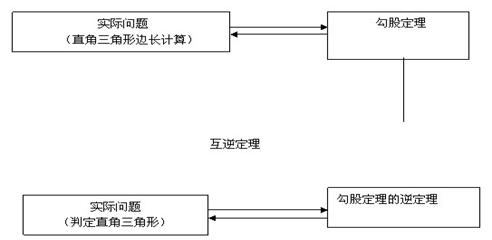
本章知识结构框图:
直角三角形是一种特殊的三角形,它有许多重要的性质,如两个锐角互余,30°的角所对的直角边等于斜边的一半。本章所研究的勾股定理,也是直角三角形的性质,而且是一条非常重要的性质。
勾股定理是几何中几个最重要的定理之一,它揭示了一个直角三角形三条边之间的数量关系,它可以解决许多直角三角形中的计算问题,是解直角三角形的主要依据之一,在生产生活实际中用途很大。它不仅在数学中,而且在其他自然科学中也被广泛地应用。
目前世界上许多科学家正在试图寻找其他星球的“人”,为此向宇宙发出了许多信号,如地球上人类的语言、音乐、各种图形等。据说我国著名数学家华罗庚曾建议,发射一种反映勾股定理的图形,如果宇宙人是“文明人”,那么他们一定会识别这种“语言”的。这个事实可以说明勾股定理的重大意义,发现勾股定理,尤其在2000多年前,是非常了不起的成就。
在第一节中,教科书让学生通过观察计算一些直角三角形两直角边为边长的小正方形的面积与以斜边为边长的正方形的面积的关系,发现两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积,从而发现勾股定理。
勾股定理的证明方法很多,教科书正文中介绍的是一种面积证法。其中的依据是图形经过割补拼接后,只要没有重叠,没有空隙,面积不会改变。在教科书中,图18.1-3(1)中的图形经过割补拼接后得到图18.1-3(3)中的图形。由此就证明了勾股定理。通过推理证实命题1的正确性后,教科书顺势指出什么是定理。
勾股定理可知,已知两条直角边的长a,b,就可以求出斜边c的长。由勾股定理可得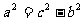 或
或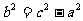 ,由此可知,已知斜边与一条直角边的长,就可以求出另一条直角边的长。也就是说,在直角三角形中,已知两条边的长,就可以求出第三条边的长。教科书相应安排了三个探究栏目,让学生运用勾股定理解决问题。
,由此可知,已知斜边与一条直角边的长,就可以求出另一条直角边的长。也就是说,在直角三角形中,已知两条边的长,就可以求出第三条边的长。教科书相应安排了三个探究栏目,让学生运用勾股定理解决问题。
在第二节中,教科书让学生画出一些两边的平方和等于第三边的平方的三角形,可以发现画出的三角形是直角三角形。从而猜想如果三角形的三边满足两边的平方和等于第三边的平方,那么这个三角形是直角三角形。这个猜想可以利用全等三角形证明,得到勾股定理的逆定理。
勾股定理的逆定理给出了判定一个三角形是直角三角形的方法。教科书安排了两个例题,让学生学会运用这种方法。这种方法与前面学过的一些判定方法不同,它通过代数运算“算”出来。实际上利用计算证明几何问题学生已经见过,计算在几何里也是很重要的。从这个意义上讲,勾股定理的逆定理的学习,对开阔学生眼界,进一步体会数学中的各种方法有很大的意义。
几何中有许多互逆的命题,互逆的定理,它们从正反两个方面揭示了图形的特征性质,所以互逆命题和互逆定理是几何中的重要概念。学生已见过一些互逆命题(定理),例如:“两直线平行,内错角相等”与“内错角相等,两直线平行”;“全等三角形的对应边相等”与“对应边相等的三角形是全等三角形”等,都是互逆命题。勾股定理与勾股定理的逆定理也是互逆的命题,而且这两个命题的题设和结论都比较简单。因此,教科书在前面已有感性认识的基础上,在第二节中,结合勾股定理的逆定理的内容的展开,穿插介绍了逆命题、逆定理的概念,并举例说明原命题成立其逆命题不一定成立。为巩固这些内容,相应配备了一些练习与习题
本章学习目标如下:
1、体验勾股定理的探索过程,会运用勾股定理解决简单问题;
(四)突破知识的难点和重点
本章的重点是反比例函数的概念、图象和性质,图象是直观地描述和研究函数的重要工具。教材中给出了大量的具体的反比例函数的例子,用以加深学生对所学知识的理解和融会贯通。本章的难点是对反比例函数及其图象和性质的理解和掌握,教学时在这方面要投入更多的精力。
尽管本章中反比例函数的内容还是比较初级的知识,但是对这些知识的掌握却是为学习后续的函数知识打下基础。因此,教学中对本章基本知识和基本技能的要求不能有丝毫降低。要适时安排适当难度的习题,以使学生对基础知识形成深刻的印象、对基本技能达到熟练的程度。
有条件的地方应尽可能使用信息技术,在本章“信息技术应用”栏目中,给出了k变化时,反比例函数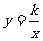 (k为常数,
(k为常数,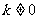 )的图象是如何变化的。尽管这一性质不是必修内容,但有兴趣和学有余力的同学却可以从中获益。
)的图象是如何变化的。尽管这一性质不是必修内容,但有兴趣和学有余力的同学却可以从中获益。
第十八章 “勾股定理”简介
本章主要内容是勾股定理及其逆定理。首先让学生通过观察得出直角三角形两条直角边的平方和等于斜边的平方的结论并加以证明,从而得到勾股定理,然后运用勾股定理解决问题。在此基础上,引入勾股定理的逆定理,并结合此项内容介绍逆命题、逆定理的概念。
本章教学时间约需8课时,具体安排如下:
18.1 勾股定理 4 课时
18.2 勾股定理的逆定理 3课时
数学活动
小结 1课时
(二)加强反比例函数与正比例函数的对比
在复习“第11章 一次函数”内容的基础上,引进本章内容。应该有意识地加强反比例函数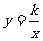 (k为常数,
(k为常数,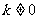 )与正比例函数
)与正比例函数 (k为常数,
(k为常数,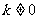 )之间的对比,对比可以从如下几方面进行:
)之间的对比,对比可以从如下几方面进行:
1、两种函数的解析式有何相同与不同?两种函数的图象的特征有何区别?
2、在常数 相同的情况下,当自变量 变化时两种函数的函数值 的变化趋势有什么区别?
3、两种函数中 的取值范围有何不同?常数 的符号改变对两种函数图象所处象限的影响如何?
回答是这样的:
1、两种函数的解析式的相同点是,自变量只有一个,即x,都有一个常数k,且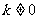 ;不同点是自变量 在解析式中的位置不同,正比例函数的解析式 的右边是一个整式,不为0的常数k是自变量x的系数,而反比例函数的解析式
;不同点是自变量 在解析式中的位置不同,正比例函数的解析式 的右边是一个整式,不为0的常数k是自变量x的系数,而反比例函数的解析式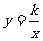 的右边是一个分式,自变量x处在分母的位置,不为0的常数k处在分子的位置。
的右边是一个分式,自变量x处在分母的位置,不为0的常数k处在分子的位置。
两种函数的图象都分布在两个象限内,这是相同之处;不同点在于正比例函数的图象是一条直线,而反比例函数的图象是两支曲线。正比例函数的图象经过原点,而反比例函数的图象不经过原点。
2、在常数 相同的情况下,当自变量x增大(减小)时,正比例函数的y值增大(减小),而反比例函数的y值减小(增大);在常数
相同的情况下,当自变量x增大(减小)时,正比例函数的y值增大(减小),而反比例函数的y值减小(增大);在常数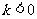 相同的情况下,当自变量x增大(减小)时,正比例函数的y减小(增大),而反比例函数的 t值增大(减小)。
相同的情况下,当自变量x增大(减小)时,正比例函数的y减小(增大),而反比例函数的 t值增大(减小)。
3、当常数的符号改变时,两类函数图象所处的象限都会随之改变。当 时,两类函数的图象都分布在一、三象限;当
时,两类函数的图象都分布在一、三象限;当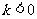 时,两类函数的图象都分布在二、四象限。
时,两类函数的图象都分布在二、四象限。
对于这些问题,不要急于给出答案,应该注意鼓励学生积极探究,在这样的氛围中,学生的数学思维和兴趣会被激发起来,对所学内容的掌握也就更牢固。
(一)注意做好与已学内容的衔接
教科书在“第11章 一次函数”已经给出了函数的一般概念以及自变量、函数值等概念.,学生对函数已经形成了初步的认识。反比例函数的教学,一方面要以前面所学的函数概念及相关知识为基础,另一方面可以反过来进一步深化对函数内涵的理解和掌握。
从学生第一次接触函数所蕴涵的“变化与对应”思想至今已经半年有余,学生对与函数相关的概念不可避免会有所遗忘或生疏。因此,学习好本章的关键是处理好新旧知识的联系,尽可能地减少学生接受新知识的困难。例如,在引进反比例函数概念时,要适时复习第11章中的函数、自变量、函数值、正比例函数、一次函数等定义或概念,为反比例函数的学习做好铺垫。这样,学生就能够比较顺利地接受和掌握反比例函数的概念和性质。
(二)注重数学思想的渗透
从数学自身的发展过程看,正是由于变量与函数概念的引入,标志着初等数学向高等数学迈进,尽管本章讲述的反比例函数仅是一种最基本、最初步的函数,但其中蕴涵的数学思想和方法,对学生观察问题、研究问题和解决问题都是十分有益的。
我们知道函数的定义不是惟一的,从不同的理解角度出发可以给出函数不同的定义。教科书在“第11章 一次函数”已经给出了函数定义,这个定义突出了数学中的变化与对应的数学思想,其内涵主要有两个:首先,两个变量互相联系,一个变量变化时另一个变量也发生变化;其次,函数与自变量之间是单值对应关系,自变量的值确定后,函数的值是唯一确定的。
在本章的编写时,一方面十分注意具体题目的分析及求解过程,另一方面更加注重一些重要的数学思想,如变化与对应的数学思想、数形结合的思想以及转化思想的传授和渗透。
(三)课程学习目标
本章内容的设计与编写以下列目标为出发点:
1、使学生理解并掌握反比例函数的概念,能根据实际问题中的条件确定反比例函数的解析式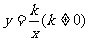 ,能判断一个给定函数是否为反比例函数;
,能判断一个给定函数是否为反比例函数;
2、能描点画出反比例函数的图象,会用代定系数法求反比例函数的解析式,进一步理解函数的三种表示方法,即列表法、解析式法和图象法的各自特点;
3.能根据图象数形结合地分析并掌握反比例函数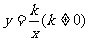 的函数关系和性质,能利用这些函数性质分析和解决一些简单的实际问题;
的函数关系和性质,能利用这些函数性质分析和解决一些简单的实际问题;
4.探索现实生活中数量间的反比例关系,在解决实际问题的过程中,进一步体会和认识反比例函数这种刻画现实世界中特定数量关系的数学模型;
5.使学生在学习一次函数之后,进一步理解常量与变量的辨证关系和反映在函数概念中的运动变化观点,进一步认识数形结合的思想方法。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com