
3.注意解题的技巧的应用,不能死算.
如:分解因式(x+1)(x+3)(x+5)(x+7)-9
=[(x+1)(x+7)][(x+3)(x+4)]-9
=(x2+8x+7)(x2+8x+15)-9
=[(x2+8x)+7][(x2+8x)+15]-9
=(x2+8x)2+22(x2+8x)+105-9
=(x2+8x)2+22(x2+8x)+96
=(x2+8x +6)(x2+8x +16)
=(x2+8x+6)(x+4)2
〈六〉、学生自我评价
[小结] 通过本节课的学习,你有什么收获和感悟?本节课,我们自己通过计算分析结果,总结出了的一些方法。在知识探索的过程中,同学们积极思考,大胆探索,团结协作共同取得了进步。
〈七〉[作业] :练习卷
2.不要将因式分解的结果又用整式的乘法展开而还原.
如: :(a2+b2)2-4a2b2
=(a2+b2+2ab)(a2+b2-2ab)
=(a+b)2(a-b)2
=[(a+b)(a-b)]2
=(a2-b2)2
=a4-2a2b2+b4
实际该题到第2个等于号就分解到底了,不能再向下
计算了!
1.因式分解应进行到底.
如:分解因式:x4-4=(x2+2)(x2-2)
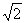
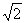 =x2+2)(x+ )(x- ).
=x2+2)(x+ )(x- ).
应在实数范围内将它分解到底.
2、我来总结:
因式分解的一般步骤
可归纳为一“提”、二“套”、三“分”、四“查”:
(1)一“提”:先看多项式的各项是否有公因式,若有必须先提出来.
(2)二“套”:若多项式的各项无公因式(或已提出公因式),第二步则看能不能用公式法用x2+(p+q)x+pq型分解.
(3)“三分”:若以上两步都不行,则应考虑分组分解法,将能用上述方法进行分解的项分成一组,使之分组后能“提”或能“套”,当然要注意其要分解到底才能结束.
(4)四“查”:可以用整式乘法检查因式分解的结果是否正确.
〈三〉、典型试题解析(师生共同完成):
[例1] 因式分解:
(1)-4x2y+2xy2-12xy;(2)3x2(a-b)-x(b-a);(3)9(x+y)2-4(x-y)2;
(4)81a4-1;(5)(x2+2x)2+2(x2+2x)+1;(6)(a2+b2)2-4a2b2.
〈四〉牛刀小试:
(1)m3+2m2-9m-18;
解:
原式=(m3+2m2)-(9m+18)
=m2(m+2)-9(m+2)
=(m+2)(m2-9)
=(m+2)(m-3)(m+3)
或者:
原式=(m3-9m)+(2m2-18)
=m(m2-9)+2(m2-9)
=(m2-9)(m+2)
=(m-3)(m+3)(m+2)
(2)a2-b2-c2-2bc;
解:
(2)原式=a2-(b2+2bc+c2)
=a2-(b+c)2
=(a+b+c)(a-b-c)
(3) x4 -5x2+4;
(3)原式=(x2)2-5(x2)+4
=(x2-4)(x2-1)
=(x-2)(x+2)(x-1)(x+1)
(4) x3-2x2-5x+6.
(4)原式=x3-x2-x2-5x+6
=x2(x-1)-(x2+5x-6)
=x2(x-1)-(x+6)(x-1)
=(x-1)(x2-x-6)
=(x-1)(x-3)(x+2)
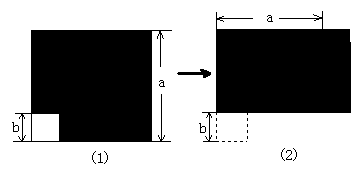
[例4] (2002·陕西)如图1,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形(如图2),通过计算两个图形阴影部分的面积,验证了一个等式,则这个等式是( ) 。
A. a2-b2=(a+b)(a-b) B.(a+b)2= a2+b2+2ab
C. (a-b)2=a2-2ab+b2 D.(a+2b)(a-b)= a2+b2-2ab

〈五〉 冒险岛:
分解因式:x3+6x2+11x+6(分组讨论)。
解:方法一:原式=x3+3x2+3x2+9x+2x+6
=x2(x+3)+3x(x+3)+2(x+3)
=(x+3)(x2+3x+2)
=(x+3)(x+1)(x+2)
方法二:原式=x3+2x2+4x2+8x+3x+6
=x2(x+2)+4x(x+2)+3(x+2)
=(x+2)(x2+4x+3)
=(x+2)(x+1)(x+3)
方法三:原式=x3+x2+5x2+5x+6x+6
=x2(x+1)+5x(x+1)+6(x+1)
=(x+1)(x2+5x+6)
=(x+1)(x+2)(x+3)
方法四:原式=(x3+5x2+6x)+(x2+5x+6)
=x(x2+5x+6)+(x2+5x+6)
=(x2+5x+6)(x+1)
=(x+2)(x+3)(x+1)
〈四〉、[学生小结]
你认为以上解题过程中,需要注意那些问题?解题过程有哪些困难?本节课有什么收获?
1、学生分组交流、讨论:
(1).因式分解的定义:把一个多项式化为n个整式的积的形式,叫做把这个
多项式因式分解式分解因式.
(2).因式分解的几种常用方法
(1)提公因式法
(2)运用公式法:
①平方差公式:a2-b2=(a+b)(a-b)
②完全平方公式:a2±2ab+b2=(a±b)2
(3)二次三项式型:x2+(a+b)x+ab=(x+a)(x+b)
(4)分组分解法:
①分组后能提公因式;
②分组后能运用公式.
8.(2008年·北京市)分解因式:
x2-4y2+x-2y= .
〈二〉、分析问题
7.(2004年·大连试验区)关于x的一元二次方程x2+bx+c=0的两根为x1=1,x2=2,则x2+bx+c分解因式的结果为: .
6.(2006年·呼和浩特)将下列式子因式分解
x-x2-y+y2= .
5.(2008年·桂林)分解因式:a3+2a2+a= 。
4.(2007年·济南)分解因式:a2-4a+4= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com