
8.(南充)已知反比例函数的图象过点(3,2)、(m,-2),则m = ;
7.(梅州)近视眼镜的度数y(度)与镜片焦距x(米)成反比,已知400度近视镜片的焦距为0.25米,则眼镜度数y与镜片焦距x之间的函数关系是 ;
6.(芜湖)函数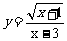 中自变量x的取值范围是
;
中自变量x的取值范围是
;
5.(南京)已知点P(x ,y)位于第二象限,且满足y≤x + 4(x,y为整数),写出一个满足上述条件的点P的坐标 ;
4.(杭州)点P在第二象限内,P到x轴的距离是4,y轴的距离是3,P的坐标是 ;
3.(济南)点P(-2,1)关于x轴对称的点的坐标为 ;
2.(泸州)已知点P(3-m,2m-4)在第一象限,则实数m的取值范围是 ;
1.(山西)已知点A(-1,2),将它先向左平移2个单位,再向上平移3个单位后得到点B的坐标是 ;
例19、(2004 重庆)如图,AB、CD是两个过江电缆的铁塔,塔AB高40米,AB的中点为P,塔底B距江面的垂直高度为6米。跨江电缆因重力自然下垂近似成抛物线形,为了保证过往船只的安全,电缆下垂的最低点距江面的高度不得少于30米。已知:人在距塔底B点西50米的地面E点恰好看到点E、P、C在一直线上;再向西前进150米后从地面F点恰好看到点F、A、C在一直线上。
(1)求两铁塔轴线间的距离(即直线AB、CD间的距离);
(2)若以点A为坐标原点,向东的水平方向为 轴,取单位长度为1米,BA的延长方向为
轴,取单位长度为1米,BA的延长方向为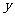 轴建立坐标系。求刚好满足最低高度要求的这个抛物线的解析式。
轴建立坐标系。求刚好满足最低高度要求的这个抛物线的解析式。

解:如图,AB=40米,BP=20米,BE=50米,BF=50+150=200(米)。
设CD的延长线交地平面于点H。
(1)设CH= ,BH=
,BH=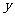
由△EBP∽△EHC得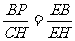 ,即
,即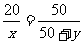 ………①
………①
由△FBA∽△FHC得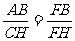 ,即
,即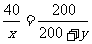 ……②
……②
由①②解得: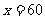 ,
,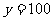
答:两铁塔轴线间的距离为100米。

(2)依题意建立坐标系如图,由(1)得CH=60米,C点比A点高20米,这时A、C两点的坐标为:A(0,0),C(100,20),设抛物线顶点为P(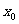 ,
,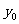 ),因为要求最低点高于地面为30-6=24(米),点A高度为40米,所以
),因为要求最低点高于地面为30-6=24(米),点A高度为40米,所以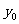 =-16。设过点A的抛物线解析式为
=-16。设过点A的抛物线解析式为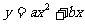 (
(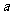 >0),则该抛物线满足
>0),则该抛物线满足
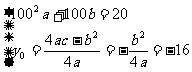
化简得: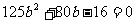 ,解得:
,解得: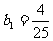 ,
,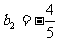
∵抛物线的对称轴在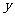 轴的右侧,有
轴的右侧,有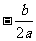 >0,而
>0,而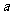 >0
>0
∴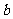 <0,故
<0,故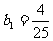 舍去
舍去
把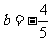 代入前式得:
代入前式得: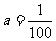
∴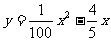
答:所求抛物线的解析式为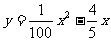 。
。
例17(2004 哈尔滨)中小学生的视力状况受到全社会的广泛关注,某市有关部门对全市4万名初中生的视力状况进行一次抽样调查统计,所得到的有关数据绘制成频率分布直方图,如下图,从左至右五个小组的频率之比依次是2:4:9:7:3,第五小组的频数是30.
(1)本次调查共抽测了多少名学生?
(2)本次调查抽测的数据的中位数应在哪个小组?说明理由.
(3)如果视力在4.9-5.1(含4.9、5.1)均属正常,那么全市初中生视力正常的约有多少人?
解:(1)因为频率之比等于频数之比,
设第一小组的频数为2k,所以各组的频数依次为2k、4k、9k、7k、3k,
于是3k=30,所以k=10
所以2k=20,4k=40,9k=90,7k=70,所以20+40+90+70+30=250(人).
答:本次调查共抽测了250名学生.
(2)中位数应在第三小组.
∵250个数据的中位数是第125和第126两个数据的平均数,
前两个小组的频数之和是20+40=60,60<125
第三小组的频数是90,90+60=150,150>126,
∴中位数应在第三小组.
(3)∵视力在4.9-5.1范围内的人有70人,
∴频率=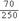 =0.28,
=0.28,
∴全市初中生视力正常的约有40000×0.28=11200(人),
答:全市初中生视力正常的约有11200人.

例18、(2004河北)为了普及环保知识,增强环保意识,某中学组织了环保知识竞赛活动,
初中三各年级根据初赛成绩分别选出了10名同学参加决赛,这些选手的决赛成绩(满分为100分)如下表所示:
|
|
决赛成绩(单位:分) |
|
初一年级 |
80 86 88 80 88 99 80 74 91 89 |
|
初二年级 |
85 85 87 97 85 76 88 77 87 88 |
|
初三年级 |
82 80 78 78 81 96 97 88 89 86 |
(1)请你填写下表:
|
|
平均分 |
众数 |
中位数 |
|
初一年级 |
85.5 |
|
87 |
|
初二年级 |
85.5 |
85 |
|
|
初三年级 |
|
|
84 |
(2)请从以下两个不同的角度对三个年级的决赛成绩进行分析:
①从众数和平均数相结合看(分析哪个年级成绩好些);
②从平均数和中位数相结合看(分析哪个年级成绩好些)。
(3)如果在每个年级参加决赛的选手中分别选出3人参加总决赛,你认为哪个年级的实力更强些?并说明理由。
解:(1)
|
年级 |
平均数 |
众数 |
中位数 |
|
初一年级 |
85.5 |
80 |
87 |
|
初二年级 |
85.5 |
85 |
86 |
|
初三年级 |
85.5 |
78 |
84 |
(2)①∵平均数都相同,初二年级的众数最高,∴初二年级的成绩好一些;
②∵平均数都相同,初一年级的中位数最高,∴初一年级的成绩好一些。
(3)∵初一、初二、初三各年级前三名学生决赛成绩的平均分分别是93分、91分、94分,∴从各年级参加决赛的选手中分别选出3人参加总决赛,初三年级的实力更强一些。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com