
3. 直线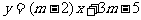 与y轴的交点在x轴上方,且y随x的增大而减小,则m的取值范围是__________。
与y轴的交点在x轴上方,且y随x的增大而减小,则m的取值范围是__________。
2. 已知反比例函数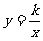 的图象在第一、三象限,则一次函数
的图象在第一、三象限,则一次函数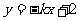 的图象不经过第___________象限。
的图象不经过第___________象限。
例:已知反比例函数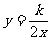 和一次函数
和一次函数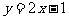 ,其中一次函数的图象经过(a,b),(a+1,b+k)两点。
,其中一次函数的图象经过(a,b),(a+1,b+k)两点。
(1)求反比例函数的解析式;
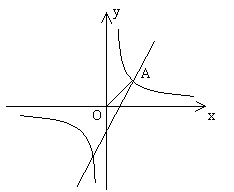
(2)如图所示,已知点A是上述两个函数的图象在第一象限的交点,求点A的坐标;
(3)利用(2)的结果,回答:在x轴上是否存在点P,使△AOP为等腰三角形?若存在,把符合条件的P点坐标都求出来;若不存在,请说明理由。
分析:(1)由一次函数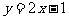 的图象经过两点(a,b),(a+1,b+k),代入消去a,b,可得k=2,进而可确定反比例函数的关系式。
的图象经过两点(a,b),(a+1,b+k),代入消去a,b,可得k=2,进而可确定反比例函数的关系式。
(2)将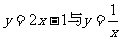 联立成方程组,易求出点A的坐标;
联立成方程组,易求出点A的坐标;
(3)应根据OA为腰和底进行分类,结合(2)探求出点P的存在性。
解:(1)依题意可得: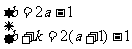
两式相减,得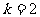
所以反比例函数的解析式为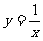
(2)由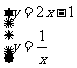 ,得
,得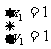 ,
,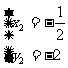
经检验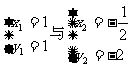 都是原方程组的解。
都是原方程组的解。
因为A点在第一象限,所以A点坐标为(1,1)
(3) ,OA与x轴所夹锐角为45°
,OA与x轴所夹锐角为45°
如图下所示①,当OA为腰时,由OA=OP,得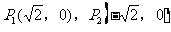
由 ,得
,得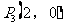
②当OA为底时,得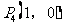
所以这样的点有4个,分别是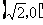 、
、
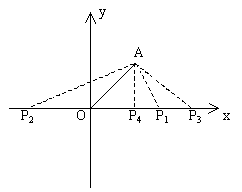
[模拟试题](答题时间:30分钟)
1. 反比例函数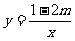 的图象上两点
的图象上两点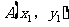 ,
,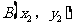 ,当
,当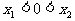 时,有
时,有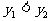 ,则m的取值范围是_____________。
,则m的取值范围是_____________。
例1. 已知一次函数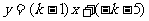 的图像经过二、三、四象限,求k的取值范围。
的图像经过二、三、四象限,求k的取值范围。
分析:直线经过二、三、四象限
则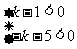
得: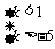
所以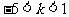
例2. 待定系数解题(转化为方程组)
如:已知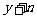 与
与 成正比例,其中m,n是常数,当
成正比例,其中m,n是常数,当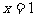 时,
时,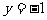 ;当
;当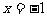 时,
时,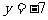 ,求y与x的函数关系。
,求y与x的函数关系。
分析:设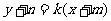
当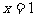 时,
时,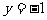 得:
得: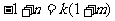
当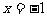 时,
时,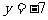 得:
得: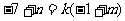
解方程组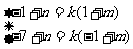
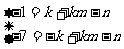
解得: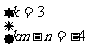
所求函数关系式为: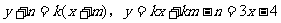
例3. 如图所示,直线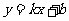 与y轴交于点A(0,3)与x轴交于点B,正方形OPQR的两边在坐标轴上,Q在直线AB上,OP:PB=1:2,求直线的解析式。
与y轴交于点A(0,3)与x轴交于点B,正方形OPQR的两边在坐标轴上,Q在直线AB上,OP:PB=1:2,求直线的解析式。
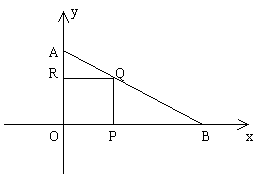
分析:求直线AB解析式,需要知道A、B坐标。而A点(0,3),则OA=3,求B点即可,即求OB长,此问题转化为几何问题。

又知PQRO为正方形,设正方形边长为x,则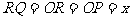

∴B点坐标为(6,0)
∴直线解析式为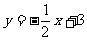
例1. 已知点N在x轴下方,且到x轴距离为2,到y轴距离为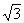 ,则点N的坐标为_________。
,则点N的坐标为_________。
分析:设点N坐标为(x,y)
由题意得: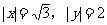
则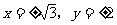
又∵点N在x轴下方,y<0
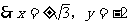
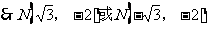
例2. 已知直线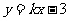 与直角坐标系的两坐标轴围成的三角形的面积为9,则直线解析式为__________。
与直角坐标系的两坐标轴围成的三角形的面积为9,则直线解析式为__________。
分析:设直线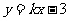 与x轴交点为A,与y轴交点为B
与x轴交点为A,与y轴交点为B
则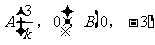
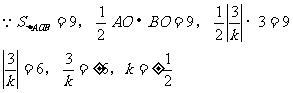
∴直线解析式为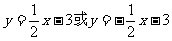
例3. 已知点A为平面直角坐标系内第四象限夹角平分线上一点,且OA=5,试在坐标轴上找一点C,使得△AOC为等腰三角形,并写出C点坐标。
分析:首先应分别在x轴和y轴上找点C
其次,△AOC应分类找:(1)OA为腰;(2)OA为底
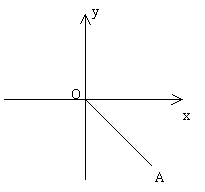
当C点在x轴上时

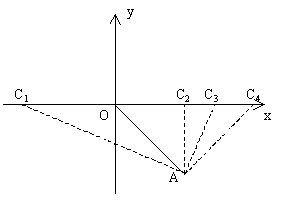
当C点在y轴上时


例1. 一次函数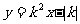 的图像经过第_______象限。
的图像经过第_______象限。
分析: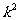 充当
充当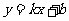 中的k,此时大于0
中的k,此时大于0
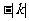 充当
充当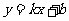 中的b,此时小于0
中的b,此时小于0
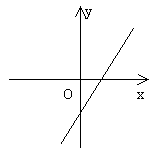
则依据直线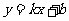 ,当
,当 的图象示意图:可知图像经过一、三、四象限。
的图象示意图:可知图像经过一、三、四象限。
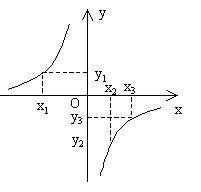
例2. 已知反比例函数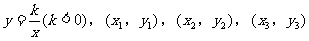 是反比例函数图象上的三个点,若
是反比例函数图象上的三个点,若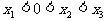 ,试判断
,试判断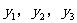 的大小关系。
的大小关系。
分析:反比例函数 的图像位于二、四象限
的图像位于二、四象限
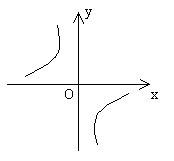
只需将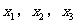 在图像上找到相对应的点,则可确定相应的函数值
在图像上找到相对应的点,则可确定相应的函数值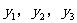 。从而根据位置判断大小。
。从而根据位置判断大小。
y轴上,越往上数越大,所以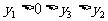 。
。
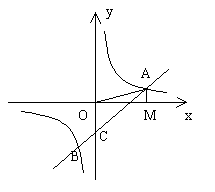
例3. 如图所示,一次函数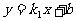 的图像过第一、三、四象限,且与双曲线
的图像过第一、三、四象限,且与双曲线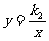 的图像交于A、B两点,与y轴交于C,
的图像交于A、B两点,与y轴交于C,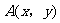 是
是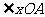 终边上的一点,若
终边上的一点,若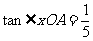 ,原点O到A点的距离为
,原点O到A点的距离为
(1)求A点坐标;
(2)求反比例函数的解析式;
(3)若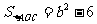 ,求一次函数的解析式。
,求一次函数的解析式。
分析:此题关键是在平面直角坐标系中借助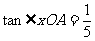 及
及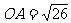 ,在Rt△中求A点坐标。从而进一步借助
,在Rt△中求A点坐标。从而进一步借助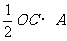 到y轴距离等于
到y轴距离等于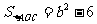 ,求出b,确定一次函数的解析式。
,求出b,确定一次函数的解析式。
解:(1)设点A坐标为(a,b),且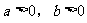
过A作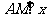 轴交x轴于M
轴交x轴于M
则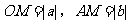
在
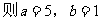
所以点A坐标为(5,1)
(2)此反比例函数解析式为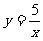
(3)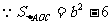 ,且
,且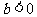 (OC=|b|,C在x轴下方)
(OC=|b|,C在x轴下方)

∴一次函数解析式为: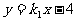
又∵直线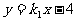 过点
过点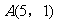
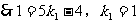
∴一次函数解析式为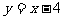
例1. 已知点P(x,x+y)与点Q(y+5,x-7)关于x轴对称,则点Q坐标为______。
分析:P点关于x轴对称时,横坐标不变,纵坐标相反
构造方程组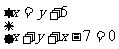
解得: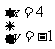
∴Q点坐标为(4,-3)
例2. 已知一次函数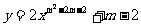 的图像经过第一、二、三象限,求m的值。
的图像经过第一、二、三象限,求m的值。
分析:一次函数条件:x的次数为1
即:
得: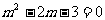
解得: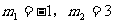
而当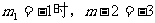
此时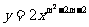 图像经过一、三、四象限
图像经过一、三、四象限
不符合题意,舍去
故m=3
例3. 已知:在△ABC中,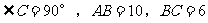 ,P为AB上一动点(P不与A、B重合),过点P作PE//BC交AC于E,连结BE,设AP=x,△BPE的面积为y,求y与x之间的函数关系,并求自变量x的取值范围。
,P为AB上一动点(P不与A、B重合),过点P作PE//BC交AC于E,连结BE,设AP=x,△BPE的面积为y,求y与x之间的函数关系,并求自变量x的取值范围。

分析: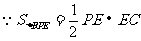
∴知道PE的长、EC的长是关键,而PE、EC与三角形相似有关。
所以此题借助比例式找出PE、EC与x之间的等量关系。
即:用含x的式子表示PE、EC,进而得到函数关系式。
解: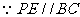
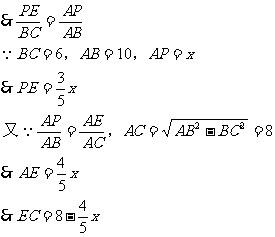

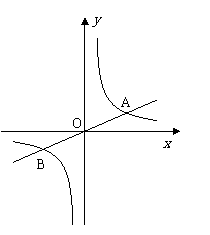
21.(14分)(福州)如图,已知直线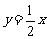 与双曲线
与双曲线 交于点A,B两点,且点A的横坐标为4.
交于点A,B两点,且点A的横坐标为4.
(1)求k的值;
(2)若双曲线 上一点C的纵坐标为8,求△AOC的面积;
上一点C的纵坐标为8,求△AOC的面积;
(3)过原点O的另一条直线l交双曲线 于P、Q两点(P在第一象限),若由点A、B、P、Q为顶点的四边形面积为24,求点P的坐标.
于P、Q两点(P在第一象限),若由点A、B、P、Q为顶点的四边形面积为24,求点P的坐标.
20.(12分)(天津改编)已知反比例函数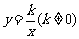 的图象与一次函数y =3x+m的图象相交于点(1,5).
的图象与一次函数y =3x+m的图象相交于点(1,5).
(1)求这两个函数的表达式;
(2)求这两个函数图象的另一个交点的坐标;
(3)作出大致图象,标出交点坐标.
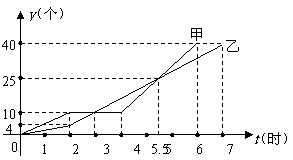
19.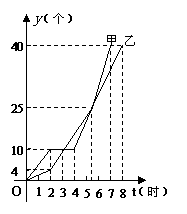 (10分)(德阳)某车间的甲、乙两名工人分别生产同种零件,他们一天生产零件y(个)与时间t(时)的函数关系如图.
(10分)(德阳)某车间的甲、乙两名工人分别生产同种零件,他们一天生产零件y(个)与时间t(时)的函数关系如图.
(1)根据图象填空:
①甲、乙中, 先完成一天的生产任务;在生产过程中,
因生产工具故障停止生产 小时;
②当t = 时,甲、乙生产的零件个数相等;
(2)谁在哪一段时间内的生产速度最快?求出该段时间内,
他每小时生产的零件个数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com