3．抛物线y=ax²+x+2经过点(-1，0)，则a=　　　 。

2．函数=y=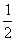(x-1)²+3，当x　　　 时，函数值y随x的增大而增大。

1．已知二次函数的图象开口向上，且顶点在y轴的负半轴上，请你写出一个满足条件的二次函数表达式：　　　　　　　　　　 。

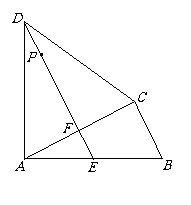
28．(8分)如图，四边形ABCD中，AD＝CD，∠DAB＝∠ACB＝90°，过点D作DE⊥AC，垂足为F，DE与AB相交于点E．

(1)求证：AB·AF＝CB·CD；

(2)已知AB＝15 cm，BC＝9 cm，P是射线DE上的动点．设DP＝x cm(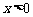)，四边形BCDP的面积为y cm²．求y关于x的函数关系式。

九年级数学(下)自主学习达标检测期中试卷

B卷

(时间90分钟 满分100分)

班级　　　　 学号　　　　 姓名　　　　 得分　　　 　

27．(8分)如图，某隧道口的横截面是抛物线形，已知路宽AB为6米，最高点离地面的距离OC为5米．以最高点O为坐标原点，抛物线的对称轴为y轴，1米为数轴的单位长度，建立平面直角坐标系，求：

(1)以这一部分抛物线为图象的函数解析式，并写出x的取值范围；

(2)有一辆宽2.8米，高1米的农用货车(货物最高处与地面AB的距离)能否通过此隧道？

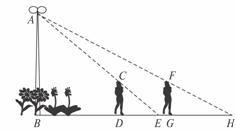
26．(8分)如图，花丛中有一路灯杆AB。在灯光下，小明在D点处的影长DE=3米，沿BD方向行走到达G点，DG=5米，这时小明的影长GH＝5米.如果小明的身高为1.7米，求路灯杆AB的高度。(精确到0.1米)

25．(6分)某商店经销一种销售成本为每千克40元的水产品.根据市场分析，若按每千克50元销售，一个月能销售500千克；销售单价每涨1元，月销售量就减少10千克.针对这种水产品的销售情况，请解答以下问题：

(1)当销售单价定为每千克55元时，计算月销售量和月销售利润.

(2)设销售单价为每千克x元，月销售利润为y元，求y与x之间的函数关系式.

(3)当销售单价定为每千克多少元时，月销售利润最大？最大利润是多少？

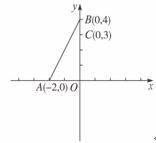
24．(6分)在直角坐标系中，已知点A(-2，0)，B(0，4)，C(0，3)，过点C作直线交x轴于点D，使得以D，O，C为顶点的三角形与△AOB相似，求点D的坐标。

23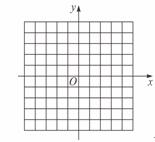．(6分)抛物线y=-x²+(m-1)x+m与y轴交于(0，3)点。

(1)求出m的值并在图中画出这条抛物线；

(2)求它与x轴的交点和抛物线顶点的坐标；

(3)x取什么值时，抛物线在x轴上方？

(4)x取什么值时，y的值随x值的增大而减小？

22．(6分)如图，等边△ABC，点D、E分别在BC、AC上，且BD=CE，AD与BE相交于点F。

(1)试说明△ABD≌△BCE；

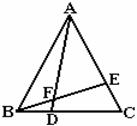(2)△AEF与△ABE相似吗?说说你的理由；

(3)BD²=AD·DF吗?请说明理由。