
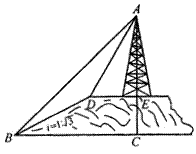
27.(8分)如图,小山的顶部是一块平地,在这块平地上有一高压输电的铁架,小山的斜坡的坡度i=1: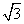 ,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为45°,在山坡的坡顶D处测得铁架顶端A的仰角为60°.
,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为45°,在山坡的坡顶D处测得铁架顶端A的仰角为60°.
(1)求小山的高度;(2)求铁架的高度.(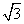 ≈1.73,精确到0.1米)
≈1.73,精确到0.1米)
26.(8分)如图,某一时刻太阳光从教室窗户射入室内,与地面的夹角∠BPC为30°,窗户的一部分在教室地面所形成的影长PE为3.5米,窗户的高度AF为2.5米.求窗外遮阳篷外端一点D到窗户上椽的距离AD.(结果精确0.1米)

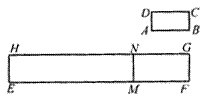
25.(6分)如图,在矩形ABCD中,AB=2AD,线段EF=10,在EF上取一点m,分别以Em、mF为一边作矩形EmnH、矩形mFGn,使矩形mFGn∽矩形ABCD.令mn=x,当x为何值时,矩形EmnH的面积S有最大值?最大值是多少?
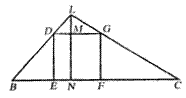
24.(6分)如图,光源L距地面(Ln)8米,距正方体大箱顶站(Lm)2米,已知,在光源照射下,箱子在左侧的影子BE长5米,求箱子在右侧的影子CF的长.(箱子边长为6米)
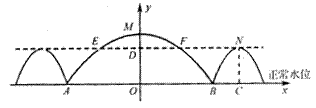
23. (6分)如图,三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小都相同.正常水位时,大孔水面宽度AB=20米,顶点m距水面6米(即mO=6米),小孔顶点n距水面4.5米(即nC=4.5米).当水位上涨刚好淹没小孔时,借助图中的直角坐标系,求此时大孔的水面宽度EF.
(6分)如图,三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小都相同.正常水位时,大孔水面宽度AB=20米,顶点m距水面6米(即mO=6米),小孔顶点n距水面4.5米(即nC=4.5米).当水位上涨刚好淹没小孔时,借助图中的直角坐标系,求此时大孔的水面宽度EF.
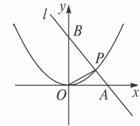
22.(6分)直线l过点A(4,0)和B(0,4)两点,它与二次函数y=ax2的图象在第一象限内交于点P,若S△AOP=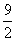 ,求二次函数关系式.
,求二次函数关系式.
21.(4分)如图,正方形ABCD中,点E是CD的中点,点F在BC上,且CF∶BC=1∶4,你能说明AE∶EF=AD∶EC吗?

20.(4分)如下图,路灯下,一墙墩(用线段AB表示)的影子是BC,小明
(用线段DE表示)的影子是EF,在m处有一颗大树,它的影子是mn。
(1) 试确定路灯的位置(用点P表示);
(2) 在图中画出表示大树高的线段;
(3) 若小明的眼睛近似地看成是点D,试画图分析小明能否看见大树。

19.(4分)计算: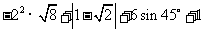
18.一个矩形剪去一个以宽为边长的正方形后,所剩下的矩形与原矩形相似,则原矩形的长与宽的比是( )
A.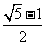 B.
B.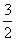 C.
C.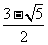 D.
D.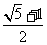
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com