
4.已知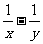 =3,则分式
=3,则分式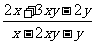 的值为_______.
的值为_______.
3.若a=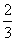 ,
,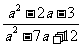 的值等于_______.
的值等于_______.
2.各分式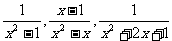 的最简公分母是
.
的最简公分母是
.
1.当x 时,分式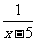 无意义、当
无意义、当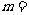 时,分式
时,分式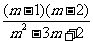 的值为零.
的值为零.
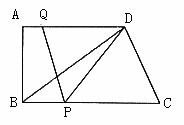
28.(8分)如图所示,在直角梯形ABCD中,AD//BC,∠A=90°,AB=12,BC=21,AD=16.动点P从点B出发,沿射线BC的方向以每秒2个单位长的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位长的速度向点D运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为t(秒).
(1)设△DPQ的面积为S,求S与t之间的函数关系式;
(2)当t为何值时,四边形PCDQ是平行四边形?
(3)分别求出出当t为何值时,① PD=PQ,② DQ=PQ?
27.(7分)(1)探究新知:
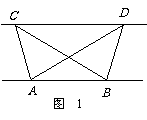
如图1,已知△ABC与△ABD的面积相等, 试判断AB与CD的位置关系,并说明理由.
(2)结论应用:
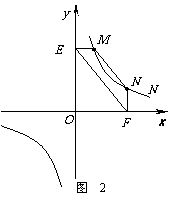
① 如图2,点M,N在反比例函数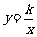 (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.
试证明:MN∥EF.
26.(6分)四川省汶川大地震后,某食品加工厂要把600吨方便面包装后送往灾区.
(1)写出包装所需的天数t天与包装速度 y 吨/天的函数关系式;
(2)包装车间有包装工120名,每天最多包装60吨,预计最快需要几天才能包装完?
(3)包装车间连续工作7天后,为更快地帮助灾区群众,厂方决定在2天内把剩余的方便面全部包装完毕,问需要调来多少人支援才能完成任务?
25.(6分)某校八年级学生开展踢毽子比赛活动,每班派5名学生参加.按团体总分多少排列名次,在规定时间每人踢100个以上(含100个)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个),经统计发现两班总分相等,此时有学生建议,可通过考查数据中的其他信息作为参考.请你回答下列问题:
|
|
1号 |
2号 |
3号 |
4号 |
5号 |
总分 |
|
甲班 |
100 |
98 |
110 |
89 |
103 |
500 |
|
乙班 |
86 |
100 |
98 |
119 |
97 |
500 |
|
|
1号 |
2号 |
3号 |
4号 |
5号 |
总分 |
|
甲班 |
100 |
98 |
110 |
89 |
103 |
500 |
|
乙班 |
86 |
100 |
98 |
119 |
97 |
500 |
|
|
1号 |
2号 |
3号 |
4号 |
5号 |
总分 |
|
甲班 |
100 |
98 |
110 |
89 |
103 |
500 |
|
乙班 |
86 |
100 |
98 |
119 |
97 |
500 |
|
|
1号 |
2号 |
3号 |
4号 |
5号 |
总分 |
|
甲班 |
100 |
98 |
110 |
89 |
103 |
500 |
|
乙班 |
86 |
100 |
98 |
119 |
97 |
500 |
|
|
1号 |
2号 |
3号 |
4号 |
5号 |
总分 |
|
甲班 |
100 |
98 |
110 |
89 |
103 |
500 |
|
乙班 |
86 |
100 |
98 |
119 |
97 |
500 |
(1)根据上表提供的数据填写下表:
|
|
优秀率 |
中位数 |
方差 |
|
甲班 |
|
|
|
|
乙班 |
|
|
|
(2)根据以上信息,你认为应该把冠军奖状发给哪一个班级? 简述理由.
24.(6分)已知:如图,在菱形ABCD中,E、F分别是BC、CD的中点.
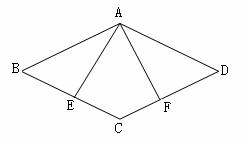 (1)求证:△ABE≌△ADF
(1)求证:△ABE≌△ADF
(2)过点C作CG∥EA交AF于H,交AD于G,若∠BAE=25°,∠BCD=130°,求∠AHC的度数.
23.(6分)一次函数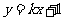 的图像与反比例函数
的图像与反比例函数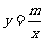 的图像交于点M(2,3)和另一点N.
的图像交于点M(2,3)和另一点N.
(1)求一次函数和反比例函数的解析式;
(2)求点N的坐标;
(3)求△MON的面积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com