
19. (本小题6分).在平面直角坐标系xOy中,直线y=-x绕点O顺时针旋转900得到直线l,直线l与二次函数y=x2+bx+2图象的一个交点为(m,3),试求二次函数的解析式.
[解析]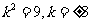 ,选C由题意,直线
,选C由题意,直线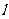 的解析式为
的解析式为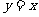 ,将
,将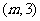 代入,解得
代入,解得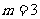 .
.
将(3,3)代入二次函数的解析式,解得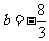
∴二次函数的解析式为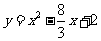 .
.
[点评]本题考查直线的旋转、直线和抛物线的交点、待定系数法,不难.
18. (本小题6分).已知关于x的方程kx2-4kx+k-5=0有两个相等的实数根,求k的值并解这个方程.
[解析]∵原方程有两个相等的实数根
∴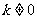 且
且
即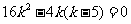
∴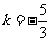 或
或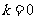 (舍)
(舍)
∴原方程可化为: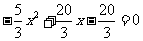
∴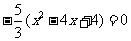
∴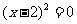
∴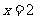
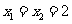 .
.
[点评]本题考查一元二次方程根的情况与判别式之间的关系,注意既然题目中说此方程有两个相等的实数根,则此方程必为一元二次方程,所以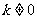 .
.
17. (本小题6分).解方程:2x2-2x-1=O
[解析]法一:原式可以变形为
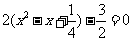
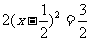
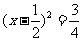
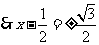
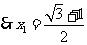
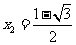 .
.
法二:应用求根公式.
[点评]本题考查一元二次方程的求解,属于基础题.
16.如图,某大学的校门是抛物线形水泥建筑物,大门的地面宽为8m,两侧距地面4m高处各有一个挂校名横匾用的铁环,两铁环的水平距离为6m,则校门的高为 m(精确到0.1m,水泥建筑物厚度忽略不计).
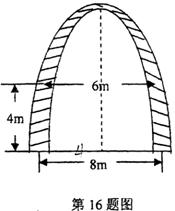
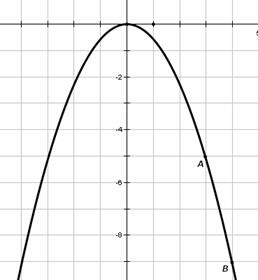
[解析]如图建立平面直角坐标系,设此抛物线的解析式为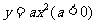 ,由题意,设
,由题意,设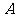 点坐标为
点坐标为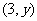 ,则
,则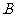 点坐标为
点坐标为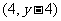 ,代入解得
,代入解得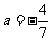 ,故此抛物线的解析式为
,故此抛物线的解析式为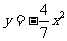 ,当
,当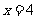 时,
时,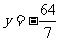 ,所以校门的高为
,所以校门的高为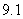 m.
m.
[点评]本题是一道实际问题,要求自己建立坐标系,然后用待定系数法求解抛物线的解析式,并要求能将抛物线上的点及坐标与题目中的实际量对应上,较难.本题建立坐标系的方法不唯一.
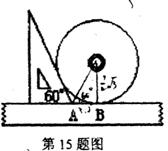
15.如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3.5cm,则此光盘的直径是 cm.
[解析]如图,设圆心为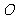 ,作
,作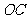 垂直三角板的斜边于
垂直三角板的斜边于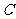 点,则△
点,则△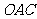 ≌△
≌△ (HL),故
(HL),故 ,
,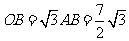 ,所以此光盘的直径是
,所以此光盘的直径是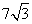 cm.
cm.
[点评]本题考查直线和圆的位置关系、三角形全等、特殊三角形的边角关系等,有一定的综合性.
14.如图,将△ABC绕着点C按顺时针方向旋转250,B点落在 位置,A点落在
位置,A点落在 位置,若
位置,若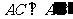 ,则∠BAC的度数是
.
,则∠BAC的度数是
.
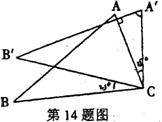
[解析]由题意, .
.
[点评]本题考查旋转、垂直等几何概念以及几何计算的能力,属于基础题.
13.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其它完全相同,小李通过多次摸球试验后发现其中摸到红色、黑色球的频率分别为O.1 5和0.45,则口袋中白色球的数目很可能是
.
[解析]因为是“多次摸球试验”以后,故口袋中白色球的数目很可能是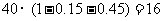 (个).
(个).
[点评]本题考查数据统计与分析的基本知识,简单.
12.己知抛物线y=3x2+4(a+1)x+3的顶点在x轴上,那么a的值是 .
[解析]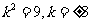 ,选C由题意可知,顶点纵坐标为0,故
,选C由题意可知,顶点纵坐标为0,故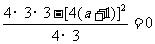 ,解得
,解得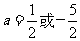 .
.
[点评]本题考查抛物线的顶点坐标公式,以及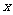 轴上的点的坐标特点,不难.
轴上的点的坐标特点,不难.
11.如果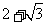 是方程x2-cx+l=0的一个根,那么c的值是
.
是方程x2-cx+l=0的一个根,那么c的值是
.
[解析]设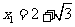 ,由于
,由于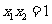 ,故
,故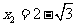 ,所以
,所以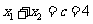 .
.
[点评]本题考查根系关系,属于基础题.
10.如上图,画有脸谱的圆与⊙0的半径相等,并绕⊙0按逆时针方向做无滑动的滚动(⊙0固定),则其中四个位置完全正确的是( )
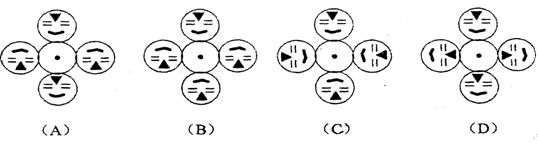
[解析]想象一下即可,选C.
[点评]本题考查旋转和想象能力,属于基础题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com