
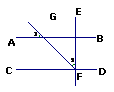
7.如图所示AB∥CD,EF⊥CD,FG平分∠EFC,则( )
(A) ∠1>∠2 (B) ∠1<∠2
(C) ∠1=∠2 (D) 不能确定

6.若两平行直线EF,MN与相交直线AB,CD相交成如
图所示的图形,与图中共有同旁内角的对数是( )
(A) 4 (B) 8
(C) 12 (D) 16
5.在y=kx+b中,当x=2时,y=8,当x=-1时,y=-7,则k , b的值是( )
(A) k=5 , b=-2 (B) k=5 , b=2 (C) k=-5 , b=-2 (D) k=–5 , b=2

4.方程x+y=4有几个正整数解( )
(A) 1个 (B) 2个 (C) 3个 (D) 4个
3.已知(a+b)2+11,(a-b)2=7,则2ab为( )
(A) 2 (B) –1 (C) 1 (D) –2
2.下列多项式的乘法中,可以用平方差公式计算的是( )
(A) (x+1)(1+x)
(B) (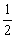 a+b)(b-
a+b)(b-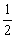 a)
a)
(C) (-a+b)(a-b) (D) (x2-y)(x+y2)
1.下列运算正确的是( )
(A) (2a-3b)2=4a2 –9b2 (B) (a+b)2=a2+b2
(C)(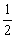 a+b)2=
a+b)2=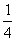 a2+ab+b2
(D)(0.3a-0.2b)2=
a2+ab+b2
(D)(0.3a-0.2b)2=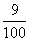 a2+
a2+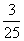 ab+
ab+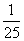 b2
b2
29. (1) 如图①,已知△ABC中,∠B > ∠C,AD⊥BC于D,AE平分∠BAC,
试证明:∠DAE = 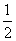 (∠B - ∠C)
(∠B - ∠C)
(2) 在图②中,其他条件不变,若把“AD⊥BC于D”改为“F是AE上一点,FD⊥BC于D”,则∠DFE与∠B、∠C有何关系?试说明理由。
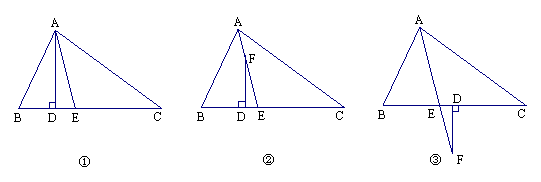 (3) 在图③中,若把(2)中的“点F在AE上”改为“点F是AE延长线上一点”,其余条件不变,则∠DFE与∠B、∠C的关系如何?(直接写出结论,不必说明理由。)
(8分)
(3) 在图③中,若把(2)中的“点F在AE上”改为“点F是AE延长线上一点”,其余条件不变,则∠DFE与∠B、∠C的关系如何?(直接写出结论,不必说明理由。)
(8分)
命题:鞠永霞 审核:袁四德 [ 01机 08春 一数期中(08.4.18) ]
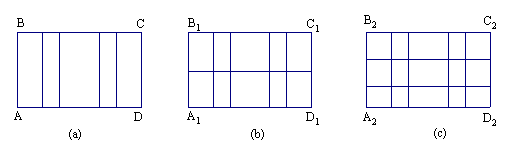
28. 如图,我们从图(a)中可以发现长方形的个数取决于把AB看作宽,看AD上有多少不同的长,所以长方形的总个数为1+2+3+4+5 = 15(个),图(b)与图(a)不相同,图(b)与图(c)也有区别,但又有相同的地方。
(1) 请你仔细观察,找出其中的规律,写出图(b)与图(c)中长方形的总个数。
(2) 如果有类似的一个长方形,其一边上有n个小格,另一边上有m个小格(这些小格的长度可以相等,也可以不等),那么你能算出这个长方形中所有长方形(包括正方形)的总个数吗?请写出答案。 (6分)
27. 如果一个正整数能够表示两个连续的偶数的平方差,那么称这个整数为“神秘数”,如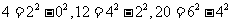 ,因此4,12,20这三个数都是神秘数。
,因此4,12,20这三个数都是神秘数。
(1) 28和2012都是“神秘数”吗?为什么?
(2) 设两个连续偶数为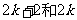 (其中
(其中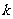 为非负整数),由这两个连续偶数构造的神秘数是4的倍数吗?为什么?
为非负整数),由这两个连续偶数构造的神秘数是4的倍数吗?为什么?
(3) 两个连续奇数的平方差(取正数)是神秘数吗?为什么? (6分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com